Управление запасами

Найти оптимальную стратегию пополнения парка автомобилей, т.е. значения и при отсутствии задержки в поставке.

Параметры задачи: тыс. руб., тыс. руб., тыс. руб., с=0. Определим критическое число 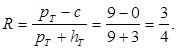Теперь найдем верхний уровень . Функция распределения впервые превысит число R при Х=6, следовательно, .

Для определения найдем наименьшее значение z, для которого последний раз выполнено неравенство

(так как с=0). Полагаем, что все денежные суммы кратны тысяче. Вычислим

Вычислим

Так как 4 ≤ 2 + 3, то .

Вычислим

Неравенство 9 ≤ 2 + 3 не выполняется, значит,

Итак, , . Отсюда следует, что при z < 5 парк автомобилей необходимо пополнить до ; при z ≥ 5 пополнять его не нужно.

Расчет планового объема поставок при вероятностном спросе с фиксированной задержкой поставки

Рассмотренные выше модели с вероятностным спросом управлялись либо стратегией «двух уровней» ,либо стратегией , когда заказ на пополнение запаса выдается через равные промежутки времени Т, а объем заказа – величина не постоянная, определяемая верхним уровнем . Переход к минимизации затрат за единицу времени по обоим параметрам стратегии обычно затруднен вследствие сложного характера зависимости распределения спроса от времени. В связи с этим при отсутствии регламентированной периодичности поставок удобно перейти к стратегии с нижним критическим уровнем и фиксированным объемом поставок.

Предположим, что недостачи товара в модели случаются редко, средняя величина дефицита мала сравнительно с q, а время его существования значительно меньше среднего интервала между поставками (при достаточно высокой цене штрафа все перечисленные условия должна выполняться). При этих предположениях средний уровень запаса составит , а затраты на содержание – в единицу времени. В каждом периоде, кроме того, будут выплачиваться стоимость заказа g и штраф, среднее значение которого составит

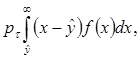
где f(x) – плотность распределения спроса за время между выдачей заказа (момент достижения ) и получением восполнения. Количество периодов в единицу времени, очевидно, равно . Следовательно, суммарные ожидаемые затраты в единицу времени могут быть подсчитаны следующим образом:

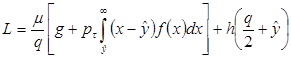. (3.12)

Приравнивая к нулю и , убеждаемся, что оптимальные параметры стратегии должны удовлетворять соотношениям

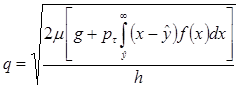(3.13)

и

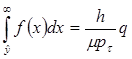. (3.14)

Указанная система уравнений легко расширяется итерационным способом: задавшись начальным значением , представляют его в (3.14) и получают . Подстановка последнего в (3.13) дает и т.д. Процесс повторяется до тех пор, пока значения параметров в последовательных итерациях не окажутся достаточно близки друг к другу. Последняя пара значений и принимается за оптимальный надор параметров. Начальное значение целесообразно определять по формуле (2.14), т.е. следует положить .

Начальное приближенное по своей величине обычно оказывается достаточно близким к конечному результату. Однако более строгим критерием качества приближенного решения является сравнение затрат. Оценим относительное увеличение затрат от неточного определения и при экспоненциально распределенном спросе за время задержки. При средней интенсивности спроса µ и задержке τ плотность распределения спроса за время τ равна 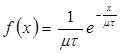, а математическое ожидание дефицита –

.

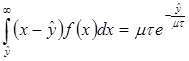Отметим, что 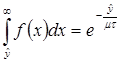. Следовательно, в нашем случае при оптимальном выборе q

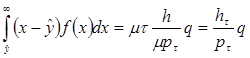. (3.15)

Подставим этот результат в (2.17), для нахождения оптимального имеем уравнение

 Скачать реферат