Гидродинамические характеристики стандартов полистиролсульфоната в растворах различной ионной силы

Для гауссовых клубков и последнее уравнение переходит в [η]=KηMaс a=0.5. Такая зависимость характеристической вязкости действительно наблюдается в идеальных растворителях.

2.1.4 Теория вращательного трения для моделей червеобразног

о ожерелья и персистентного цилиндра

Червеобразное ожерелье

Вращательное трение червеобразной цепи было рассмотрено Хирстом, использовавшим и развившим формализм, разработанный Кирквудом, в его теории вращательного трения палочкообразного ожерелья.

Положение центров гидродинамического сопротивления (бусинок) с коэффициентом трения ж в используемой Хирстом модели определяется в молекулярной системе координат XYZ, начало которой совмещено со средней точкой молекулярной цепи, а направление оси Z совпадает с направлением цепи в этой точке. Предполагается цилиндрически-симметричное распределение элементов цепи с осью симметрии Z. Применяя методы, разработанные для червеобразной цепи, Хирст вычислил - средние квадраты координат -го элемента цепи, удаленного по контуру цепи на расстояние Li от начала координат:

(25)

(26)

Эти выражения в области малых переходят в соотношения

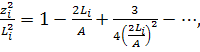(27)

(28)

Откуда, при следует и , что соответствует конформации прямой тонкой палочки. В области следует , что соответствует гауссову клубку с распределением сегментов, в средней сферически-симметричным относительно средней точки цепи.

Окончательные выражения для коэффициента вращательного трения W червеобразной цепи при ее вращении вокруг оси X или Y Хирст получает для двух предельных случаев.

Для коротких цепей, когда (слабо изогнутая палочка):

(29)

Для длинных цепей, когда (червеобразный клубок),

(30)

Если выразить через диаметр эквивалентной стоксовой сферы и принять модель червеобразного ожерелья с соприкасающимися бусами , то последние выражения трансформируются в выражения

(31)

(32)

Эти выражения отличаются от формул Кирквуда для палочкообразного ожерелья наличием члена, пропорционального . Этот член характеризует уменьшение вращательного трения слабо изогнутой палочки по сравнению с прямолинейной за счет ее гибкости.

Эта молекулярная модель была использована также при вычислении характеристической вязкости червеобразной цепи. Поскольку применяемая модель молекулы асферична, необходимо определит функцию с распределения молекул по ориентациям в сдвиговом поле потока. С этой целью решается уравнение вращательной диффузии, полученное Петерлином

(33)

Полученное решение, как и следовало ожидать для молекул с цилиндрической симметрией, совпадает с результатом Петерлина. Выражения для характеристической вязкости в предельных случаях короткой и длинной червеобразной цепи, согласно Хирсту и Тагами, имеют следующий вид:

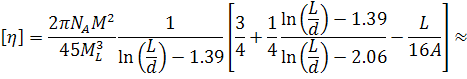
(34)

(35)

Первое из которых при очень больших значениях (тонкая червеобразная цепь) и переходит в формулу Кирквуда для палочкообразного ожерелья с соприкасающимися бусами.

Все это показывает, что модель ожерелья, введенная Кирквудом для описания гидродинамического взаимодействия и характеристики гидродинамических свойств цепных молекул, может быть использована в применении к макромолекулам с различной конформацией – от прямолинейной палочки до гауссова клубка. При этом оказывается, что при увеличении длины молекулярной цепи для палочкообразных молекул гидродинамическое взаимодействие растет пропорционально логарифму их длины, а для гауссовых клубков – пропорционально корню квадратному из длины цепи.

Персистентный цилиндр

Под червеобразным (персистентным) цилиндром понимают цилиндр, изогнутый таким образом, что форма его осевой линии описывается уравнением червеобразной цепи

(36)

и соответственно расстояние между любыми двумя его точками на осевой линии определяется по формуле

(37)

Гидродинамическое сопротивление, испытываемое таким телом при его движении в вязкой жидкости, вычисляется методом Озеена – Бюргерса.

Теория характеристической вязкости раствора жесткоцепных молекул на основе модели червеобразного цилиндра была разработана Ямакавой, применившим для этой цели метод Озеена – Бюргерса.

В первоначальном варианте были проведены вычисления характеристической вязкости без учета краевых эффектов. В дальнейшем они были дополнены теорией, учитывающей края червеобразного цилиндра, что существенно для области малых значений , когда молекула имеет форму слабоизогнутой палочки конечной толщины . Таким образом, для этой области фрикционные свойства молекул могут быть описаны комбинацией теории прямого сфероцилиндра, учитывающей конечность , и теории червеобразного цилиндра, учитывающей гибкость (конечную величину ) молекулярной цепи.

 Скачать реферат