Разложение функций. Теория вероятностей

Теорема.

Вероятность появления хотя бы одного из событий А1, А2…, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий, т.е.

Р(А)=1-q1q2…qn

Замечание.

Если все события имеют одинаковую вероятность Р, то

Р(А)=1-qn.

Примеры 82, 87, Д/з.

Формула полной вероятности.

События В1,В2,…,Вn являются несовместимыми и

образуют полную группу, т.е. Р(В1)+ Р(В2)+…+ Р(Вn)=1. И пусть событие А может наступить лишь при появлении одного из событий В1,В2,…,Вn. Тогда вероятность события А равна сумме вероятностей каждого из этих событий на соответствующую условную вероятность события А.

Р(А)=Р(В1)РВ1(А)+ Р(В2)РВ2(А)+…+ Р(Вn)РВn(А)

Формула Бейеса

События В1,В2,…,Вn являются несовместимыми и образуют полную группу, т.е. Р(В1)+ Р(В2)+…+ Р(Вn)=1. И пусть событие А может наступить лишь при появлении одного из событий В1,В2,…,Вn. Тогда вероятность события А находится по формуле полной вероятности.

Пусть событие А уже произошло. Тогда вероятности гипотез В1,В2,…,Вn могут быть переоценены по формуле Бейеса:

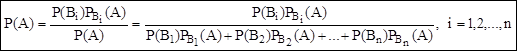
Формула Бернулли

Пусть производится n независимых испытаний, в каждом из которых событие А может или наступить или не наступить. Вероятность наступления (не наступления) события А одна и та же и равна p (q=1-p).

Вероятность того, что в n независимых испытаниях событие А наступит ровно к раз (по фиг, в какой последовательности), находится по формуле Бернулли:

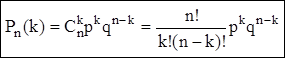
Вероятность того, что в n независимых испытаниях событие наступит:

а). Менее к раз Pn(0)+Pn(1)+…+Pn(k-1).

б). Более к раз Pn(k+1)+Pn(k+2)+…+Pn(n).

в). не менее к раз Pn(k)+Pn(k+1)+…+Pn(n).

Г). не более к раз Pn(0)+Pn(1)+…+Pn(k).

Локальная и интегральная теоремы Лапласа.

Этими теоремами мы пользуемся в том случае, когда n достаточно большое.

Локальная теорема Лапласа

Вероятность того, что в n независимых испытаниях событие наступит ровно ‘к’ раз, приближенно равно:

,

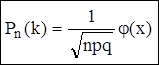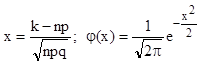
Таблица функций для положительных значений (х) приведена в задачнике Гмурмана в Приложении 1, стр.324-325.

Так как четная (), то для отрицательных значений (х) пользуемся той же самой таблицей.

Интегральная теорема Лапласа.

Вероятность того, что в n независимых испытаниях событие наступит не менее ‘к’ раз, приближенно равно:

,

Функция Лапласа

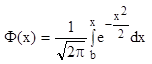
Таблица функций для положительных значений [5<=x<=5] приведена в задачнике Гмурмана в Приложении 2, стр.326-327. Для значений, больших 5 полагаем Ф(х)=0,5.

Так как функция Лапласа нечетная Ф(-х)=-Ф(х), то для отрицательных значений (х) пользуемся той же самой таблицей, только значения функции берем со знаком минус.

Закон распределения вероятностей дискретной случайной величины

Биноминальный закон распределения.

Дискретная – случайная величина, возможные значения которой есть отдельные изолированные числа, которые эта величина принимает с определенными вероятностями. Другими словами, возможные значения дискретной случайной величины можно пронумеровать.

Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Дискретные случайные величины обозначаются большими буквами Х, а их возможные значения – маленькими х1, х2, х3…

Например.

Х – число очков, выпавших на игральной кости; Х принимает шесть возможных значений: х1=1, х2=1, х3=3, х4=4, х5=5, х6=6 с вероятностями р1=1/6, р2=1/6, р3=1/6 … р6=1/6.

Законом распределения дискретной случайной величины называют перечень ее возможных значений и соответствующих им вероятностей.

Закон распределения может быть задан:

1. в виде таблицы.

2. Аналитически - в виде формулы.

3. графически. В этом случае в прямоугольной системе координат ХОР строятся точки М1(х1,р1), М2(х2,р2), … Мn(хn,рn). Эти точки соединяют отрезками прямых. Полученную фигуру называют многоугольником распределения.

Для написания закона распределения дискретной случайной величины (х), надо перечислить все ее возможные значения и найти соответствующие им вероятности.

Если соответствующие им вероятности находятся по формуле Бернулли, то такой закон распределения называется биномиальным.

Пример №168, 167, 171, 123, 173, 174, 175.

Числовые значения дискретных случайных величин.

Математическое ожидание, дисперсия и среднее квадратичное отклонение.

Характеристикой среднего значения дискретной случайной величины служит математическое ожидание.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на их вероятности. Т.е. если задан закон распределения, то математическое ожидание

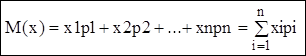
Если число возможных значений дискретной случайной величины бесконечно, то

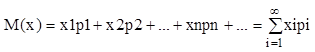
Причем ряд, стоящий в правой части равенства, сходится абсолютно, и сумма всех вероятностей рi равна единице.

Свойства математического ожидания.

1. М(С)=С, С=пост.

2. М(Сх)=СМ(х)

3. М(х1+х2+…+хn)=М(х1)+М(х2)+…+М(хn)

4. М(х1*х2*…*хn)=М(х1)*М(х2)*…*М(хn).

5. Для биноминального закона распределения математическое ожидание находится по формуле:

М(х)=n*р

Характеристикой рассеяния возможных значений случайно величины вокруг математического ожидания служат дисперсия и среднее квадратичное отклонение.

Дисперсией дискретной случайной величины (х) называют математическое ожидание квадрата отклонения. Д(х)=М(х-М(х))2.

Дисперсию удобно вычислять по формуле: Д(х)=М(х2)-(М(х))2 .

Свойства дисперсии.

1. Д(С)=0, С=пост.

2. Д(Сх)=С2Д(х)

3. Д(х1+х2+…+хn)=Д(х1)+Д(х2)+…+Д(хn)

4. Дисперсия биноминального закона распределения

Д(х)=nрq

Средним квадратичным отклонением случайной величины называют квадратный корень из дисперсии.

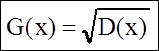
примеры. 191, 193, 194, 209, д/з.

Интегральная функция распределения (ИФР, ФР) вероятностей непрерывной случайной величины (НСВ). Непрерывная – величина, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Число возможных значений НСВ естьи его невозможно перенумеровать.

 Скачать реферат