Задачи на отыскание наибольшего и наименьшего значения функции

Анализ учебников

Требования Госстандарта образования к умениям и навыкам учащихся гласят, что учащиеся должны уметь:

- вычислять производные и первообразные элементарных функций, используя справочные материалы;

- исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с

использованием аппарата математического анализа;

- вычислять в простейших случаях площади с использованием первообразной;

- использовать приобретенные знания и умения в практической деятельности и повседневной жизни для решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения;

- применять аппарат математического анализа к решению задач.

Исходя из требований стандарта можно сделать вывод, что учащиеся должны владеть элементарными навыками математического моделирования и в частности, уметь применять математический аппарат при решении задач на отыскание наибольших и наименьших значений различных величин при заданных условиях. Таким образом, реализуется прикладная направленность обучения математике, и осуществляются межпредметные связи с другими дисциплинами. В первую очередь учащиеся должны владеть универсальным методом решения задач на оптимизацию, методом, включающим в себя построение некоторой функции и отыскание ее экстремумов с помощью производной.

Рассмотрим, как данную тему вводят такие авторы учебников как Мордкович А.Г., Колмогоров А.Н., Башмаков М.И.

Сначала рассмотрим серию учебников под редакцией А.Г. Мордковича.

В 7 классе учащиеся первый раз сталкиваются с задачами на экстремум при изучении координатной прямой. Здесь им приходится решать задачи на нахождение наибольшего и наименьшего числа на взятом промежутке, нахождение наибольших и наименьших значений функций на отрезке. Вот пример одной из таких задач:

Укажите наибольшее число, принадлежащее промежутку а) [-15; -11];

б) [5; 7); в) [5; 7].

Так же в 7 классе а теме «Линейная функция» Мордкович А.Г. вводит само понятие наибольшего и наименьшего значения функции на отрезке. Он рассматривает линейную функцию y = на отрезке [0;6].

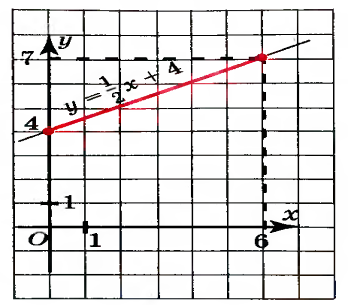
Рис. 1

Соответствующий отрезок графика выделяется на чертеже. Замечается, что самая большая ордината у точек, принадлежащих выделенной части, равна 7 - это и есть наибольшее значение заданной линейной функции на отрезке. Записывается это следующим образом . Далее отмечается, что самая маленькая ордината у точек, принадлежащих выделенной на рисунке части прямой, равна 4 - это и есть наименьшее значение линейной функции на отрезке [0; 6]. Записывают так .

В 8 и 9 классах учащиеся продолжают сталкиваться с задачами на нахождение наибольшего и наименьшего значения при изучении квадратичной функции, функции y =, у = (8 класс) и при изучении темы «Неравенства» (9 класс). Здесь ученикам приходится решать задачи, как на нахождение наименьшего числа удовлетворяющего системе уравнений, нахождение наименьшего и наибольшего значения функций вида у= на отрезке.

Приведём несколько примеров:

(8 класс). Постройте график функции у = . С помощью графика найдите:

а) значения у при х = 4; 7; 16;

б) значения х, если у = 0; 1; 3;

в) наименьшее и наибольшее значения функции на отрезке [0; 4];

г) при каких значениях х график функции расположен выше прямой

у = 1; ниже прямой у = 1.

(8 класс) Найдите наименьшее и наибольшее значения функции y=:

а) на отрезке [0; 4];

б) на луче [3; +);

в) на отрезке [1; 9];

г) на полуинтервале (2; 9].

(8 класс) Постройте график функции у = . С помощью графика найдите:

а) значения у при х = -3; 1; 6;

б) значения х если у = 3; -1; -6;

в) наименьшее и наибольшее значения функции на отрезке [-3; -1];

(9 класс) Решите двойное неравенство 0<1+4x<17 и укажите наименьшее и наибольшее целые числа, которые являются его решениями.

(9 класс) Найдите наименьшее целое число, удовлетворяющее системе неравенств

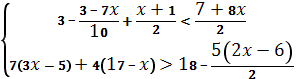
В 10 же классе Мордкович А.Г. посвящает теме целый параграф под названием «Применение производной для отыскания наибольших и наименьших значений величин», который состоит из 2 пунктов:

•Отыскание наибольшего и наименьшего значений непрерывной функции на промежутке;

•Задачи на отыскание наибольших и наименьших значений величин.

В первом пункте параграфа рассматривается нахождение наибольшего и наименьшего значения функции на отрезке. Автор отмечает, что производная используется в тех случаях, когда графически или с помощью рассуждений отыскать наибольшее и наименьшее значения функции невозможно. Потом автор говорит о ряде теорем из курса математического анализа, которые приводятся без доказательства:

Если функция непрерывна на отрезке, то она достигает на нём и своего наибольшего, и своего наименьшего значений.

Наибольшего и наименьшего значений непрерывная функция может достигать как и на концах отрезка, так и внутри него.

Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.

Далее в данном пункте приведен алгоритм нахождения наибольшего и наименьшего значения функции на отрезке:

1. Найти производную.

2. Найти стационарные и критические точки функции, лежащие внутри отрезка.

3. Вычислить значения функции в точках, отобранных на втором шаге, и на концах отрезка; выбрать среди этих значений наименьшее (это будет наименьшее значение) и наибольшее (это будет наибольшее значение).

Так же в этом пункте автор говорит о нахождении наибольшего и наименьшего значений функции на интервале. Он приводит следующую теорему:

Пусть функция y = f(x) непрерывна на промежутке X и имеет внутри него единственную стационарную или критическую точку x = x0. Тогда:

а) если x = x0 – точка максимума, то yнаиб.=f(x0);

б) если x = x0 – точка минимума, то yнаим.=f(x0).

После которой разобран пример.

Во втором пункте параграфа автор рассматривает уже текстовые задачи, в которых требуется найти наименьшее или наибольшее значение какой-либо величины. Такие задачи он называет задачами на оптимизацию (от латинского слова optimum – «наилучший»). В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причем надо найти такое значение второй величины, при котором первая принимает свое наибольшее или наименьшее (наилучшее в данных условиях) значение. Для решения задач на оптимизацию Мордкович А. Г. предлагает схему из трех этапов математического моделирования: