Статистические методы анализа динамики численности работников

,

где ymax и ymin – максимальное и минимальное значения признака.

чел.

Величина интервала равна 20,0. Отсюда путем прибавления величины интервала к минимальному уровню признака в группе получим следующие группы организаций по среднесписочной численности (

таблица 2.3.).

Таблица 2.3.

Данные группировки показывают, что 63,3 % организаций имеют среднесписочную численность работников менее 180 чел.

Мода (Мо) – это значение случайной величины, встречающееся с наибольшей вероятностью в дискретном вариационном ряду – это вариант, имеющий наибольшую частоту. В интервальном вариационном ряду мода вычисляется по формуле:

,

где y0 – нижняя граница модального интервала;

h – размер модального интервала;

fMo – частота модального интервала;

fMo-1 – частота интервала, стоящего перед модальной частотой;

fMo+1 – частота интервала, стоящего после модальной частоты.

Отсюда: чел.

Графическое нахождение моды:

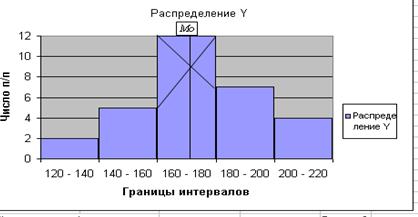
Медиана (Ме) – это величина признака, который находится в середине ранжированного ряда, то есть расположенного в порядке возрастания или убывания.

Для интервального вариационного ряда Ме рассчитывается по формуле: ,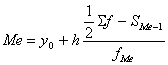

где y0 – нижняя граница медианного интервала;

h – размер медианного интервала;

- половина от общего числа наблюдений;

SMe-1 – сумма наблюдений, накопленная до начала медианного интервала;

fMe – частота медианного интервала.

Определяем медианный интервал, в котором находится порядковый номер медианы (n).

В графе «Сумма накопленных наблюдений» таблицы 2.4. значение 15 соответствует интервалу №3, то есть 160 – 180. Это и есть медианный интервал, в котором находится медиана.

Отсюда: 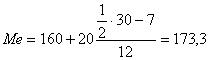чел.

Таблица 2.4.

Графическое нахождение медианы:

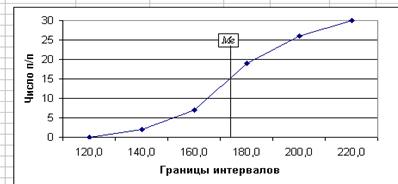
Рассчитаем характеристики ряда распределения.

Для расчета необходимо определить середины интервалов распределения среднесписочной численности работников (таблица 2.5.).

Таблица 2.5.

 Скачать реферат