Построение модели поведения потребителя в условиях совершенной конкуренции

Далее следует определить параметры модели:

х1 – количество потребляемых благ первого вида,

х2 – количество потребляемых благ второго вида,

b1,b2 – коэффициенты предпочтительности благ, первого и второго вида соответственно,

R – доход потребителя,

S – функция полезности потребителя,

p1 и p2 – цена на первое и второе благо соответственно.

Затем, внесем определенные д

анные в таблицу.

В ячейку I2 введем формулу: =H2*D2^F2*E2^G2

В ячейку J2: =A2*D2

В ячейку К2: =B2*E2

В ячейку L2: =F2+G2

В ячейку М2: =J2+K2

Надстройка «Поиск решения» позволяет при заданных ограничениях определить количества благ х1 и х2 рис.2. Для этого целевой ячейкой указываю ячейку S, равной максимальному значению. Изменяем ячейки х1 и х2 далее задаем ограничения (см. рис2). После задания всех ограничений необходимо нажать кнопку Выполнить в надстройке «Поиск решения».

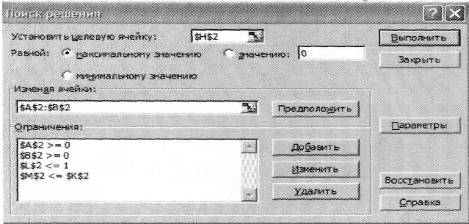
Рис. 2

4 Программная реализация экономико-математической модели и метода ее анализа

Построим модель поведения потребителя в зависимости от изменения цен. Цены варьируются в диапазоне от: цена на первое благо изменяется от 20 до 24 единиц, а на второе от 15 до 21. Доход остается неизменным и равным 750 единиц. А коэффициенты предпочтительности благ равны 0,35 и 0,45 соответственно.

После выполнения поиска решений получим модель потребительского вида представленную в табл. 2

Табл. 2

 Скачать реферат