Транспортные задачи

Задача №1

Исходные данные

Решение

Для сформулированной задачи транспортная таблица имеет вид:

В клетке транспортной таблицы записываются стоимости перевозок из пунктов отправления Аi (i = 1, 2, 3, 4) в пункты назначения Bj (j = 1, 2, 3, 4, 5). Находится начальное опорное решение методом минимальной стоимости. Для этого запасы в Аi пунктов отправления распределяются в соответствии с заявками Bj пунктов назначения и заполняются клетки с минимальными стоимостями перевозок. При этом все запасы должны быть распределены в соответствии с заявками. Вычислим затраты для этого опорного решения.

Z1 = C11 * X11 + C13 * X13 + C15 * X15 + C22 * X22 + C24 * X24 + C32 * X32 + C33 * X33 + C35 * X35 + C41 * X41 + C44 * X44 =

= 349

Для определения сомножителя опорного решения необходимо найти потенциалы заполненных клеток.

Сумма потенциалов равна стоимости перевозок

A1 + B1 =3

A1 + B3 = 1

A1 + B5 = 4

A2 + B2 = 6

A2 + B4 = 1

A3 + B2 = 5

A3 + B3 = 8

A3 + B5 = 2

A4 + B1 = 5

A4 +B4 = 2

Система состоит из 10 уравнений и имеем 9 переменных. Система неопределенная. Поэтому одному из потенциалов задаем произвольное значение. Пусть A1 = 3

Тогда:

B1 = 0

B3 = -2

B5 = 1

A3 = 7

A4 = 5

B4 = -3

A2 = 4

B2 = -2

Значение потенциалов записываем в таблицу рядом с Аi и Bj

Проверяем опорное решение на оптимальность для всех незаполненных клеток таблицы

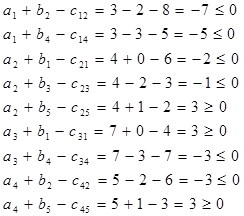
Начальное опорное решение не является оптимальным, т.к. имеется положительная оценка в A4B5, A3B1, A2B5.

Переходим к новому опорному решению. Необходимо осуществить сдвиг по циклу A4B5 – A2B5. Получим следующую транспортную таблицу.

Вычислим значение целевой функции на этом опорном решении: Z2=369. Составим уравнения, аналогичные (1)

A1 + B1 =3

A1 + B3 = 1

A1 + B5 = 4

A2 + B2 = 6

A2 + B4 = 1

A3 + B2 = 5

A3 + B3 = 8

A3 + B5 = 3

A4 + B1 = 5

A4 +B4 = 2

Система опять состоит из восьми уравнений и имеет девять переменных. Одному из потенциалов задаем произвольное значение а4 =0. Тогда,

A1 = 3

A2 = 4

A3 = 10

A4 = 5

B1 = 0

B2 = 2

B3 = -2

B4 = -3

B5 = 1

Проверяем опорное решение на оптимальность. С этой целью вычисляем оценки для всех незаполненных клеток таблицы

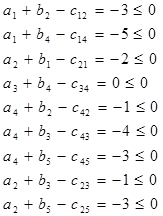
Все оценки не положительны. Следовательно, решение является оптимальным, значение целевой функции: Z2=369.

Задача №2

Исходные данные:

Таблица возможных перемещений:

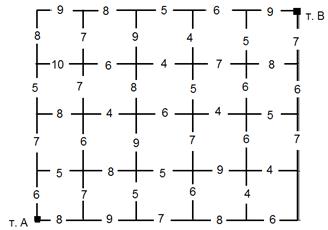
Решение

Динамическое программирование специально приспособленное к так называемым многошаговым операциям.

 Скачать реферат