Финансовые функции и рекурсия

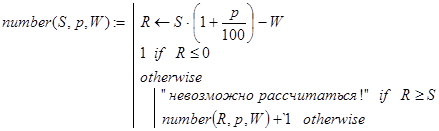(38)

Разберем еще один вариант решения данной задачи. Пусть a=1+p/100. Тогда:

- долг через 1 период;

- долг через 2 периода;

… … …

- долг через k периодов;

Отсюда, прежде всего, вытекает, что с долгом удастся расплатиться, если S×p/100<W, то есть его увеличение за первый период должно быть меньше разового платежа. Впрочем, это было ясно и из предыдущих рассуждений. Далее, последнее соотношение говорит о том, что при S×p/100<W долг будет погашен через k периодов, где k - наименьшее натуральное число, удовлетворяющее неравенству:

Рассмотрим рекурсивную функцию number1(S,p,W,k):

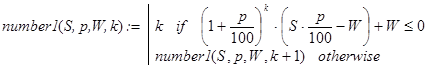(39)

с некоторым вспомогательным натуральным аргументом k. Ясно, что при обращении к ней с любыми значениями S, p и W (S×p/100<W) и k=1 получим решение исходной задачи. Обратите внимание на отсутствие отложенных вычислений при реализации number1(S,p,W,k).

Контрольные примеры.

Замечание. Из предыдущих рассуждений вытекает, что решение задачи 16 можно получать так. Вычислить значение функции

(логарифм десятичный) и взять наименьшее целое, большее или равное num(S,p,W).

Рассмотрим еще одну задачу, проливающую свет на то, как банки “делают деньги”. Пусть имеется система из n банков B1, B2, ., Bn, для каждого из которых установлена норма резервов в p процентов. Это означает, что любой из этих банков p процентов своих наличных денег должен хранить в некотором Центральном банке B0 в виде обязательных резервов. Остальные деньги являются свободными резервами банков. Их можно давать в кредит под определенные проценты, вкладывать в различные проекты, а из полученных доходов выплачивать вкладчикам проценты за пользование их деньгами.

Задача о суммарной способности к кредитованию

Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2, .,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2, .,n-1), а норма обязательных резервов равна p процентов. Определить суммарную способность к кредитованию рассматриваемой системы банков.

Решение. Получить решение данной задачи можно по рекурсивной функции credit(S,p,n). Декомпозиция в ней реализована, исходя из следующей посылки. Суммарная величина кредитования всей системы банков складывается из величины кредитования банка B1 и суммы величин кредитования остальных банков с учетом того, что вклад в банк B2 составил S×(1-p/100) денежных единиц. База рекурсии также очевидна: нет банков (n=0) - нет кредитования.

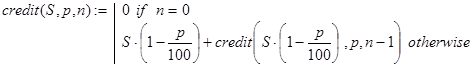
Вывод конечной формулы для решения задачи (10) может быть проведен так:

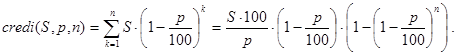(40)

Контрольные примеры.

Какие же выводы можно сделать из рассмотрения последней задачи? В системе коммерческих банков B1, B2, ., Bn не предполагалось, что все они различны. Более того, допустим и такой крайний случай: B1 = B2 = . = Bn. Поэтому способность системы банков к кредитованию, вообще говоря, не связана с их количеством. Но эта способность существенно связана с оперативным возвратом отдаваемых в кредит денег, после серии сделок с ними, снова в банки в виде вкладов. Кроме того ясно, как центральный банк путем изменения ставки обязательных резервов может влиять на суммарный объем кредитования. Если процент обязательных резервов растет, то суммарная величина кредитов убывает, если же этот процент уменьшается, то суммарная величина кредитов возрастает.

Задача о минимальном количестве банков

Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2, .,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2, .,n-1), а норма обязательных резервов равна p процентов. Определить минимальное количество n системы банков Bk (k=1,2, .,n), для которых суммарная способность к кредитованию не меньше заданной величины H.

Решение. Здесь, как и в предыдущей задаче, не предполагается, что все банки Bk (k=1,2, .,n) различны. Поэтому фактически речь идет не о минимальном количестве банков, обеспечивающих кредитование, не меньшее заданной величины H, а о минимальном количестве (оперативных) возвратов в банки денег, отдаваемых в кредит. Но нам удобней вести речь о количестве банков. Прежде всего, из общей формулы (40) вытекает, что данная задача не всегда имеет решение. При бесконечной системе банков предельная сумма кредитования равна L(S,p) = (S×100/p) ×(1-p/100). Поэтому решать задачу можно лишь при условии H<L(S,p). Найти n можно, как наименьшее натуральное решение неравенства

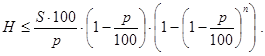
Мы будем вычислять n с помощью функций findn() и num():

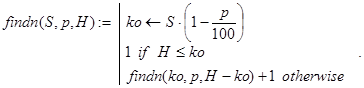
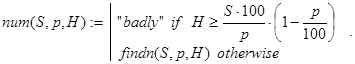
Декомпозиция в рекурсии для findn(S,p,H) организована по величинам оставшегося неудовлетворенным кредита по мере увеличения числа банков в системе.

Контрольные примеры.

Задача о изменении величины суммарного кредитования

Пусть в банк B1 внесен вклад в S денежных единиц. Будем считать, что свободные резервы банка Bk (k=1,2, .,n-1) в результате ряда операций становятся вкладом в банк Bk+1 (k=1,2, .,n-1), а норма обязательных резервов установлена в p (0<p<100) процентов. Изменить ставку p так, чтобы суммарная величина кредитов, предоставляемых всеми банками, изменилась в a>0 (a¹1) раз, то есть либо увеличилась в a раз при a>1, либо уменьшилась в 1/a раз при 0<a<1.

Решение. Сразу отметим, что как и в предыдущей задаче не предполагается, что все банки Bk (k=1,2, .,n) различны. Задача, по-видимому, не всегда имеет решение. Если решение x есть, то как его искать? На помощь может прийти формула (40). В соответствии с ней имеем:

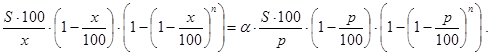
Сократим обе части этого соотношения на S×100 и, обозначив правую часть через b:

для нахождения решений задачи получим уравнение:

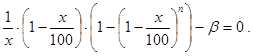(41)

 Скачать реферат