Взаимозаменяемость продовольственных продуктов - масла животного и масла растительного. Их потребление

Оценка статистической значимости коэффициентов регрессии и коэффициента корреляции

Оценим статистическую значимость полученных коэффициентов регрессии а0 и а1, коэффициента корреляции rух с помощью t-критерия Стьюдента на уровне значимости d=0,05.

Эта проверка проводится по единой схеме, с помощью гипотез.

Выдвигается нулевая гипотеза Н0 о случайной природе полученного коэффи

циента, о незначимом его отличии от нуля, то есть гипотеза Н0 состоит в том, что коэффициент=0. Альтернативная ей гипотеза Н1 состоит в том, что неслучайно, то есть полученный коэффициент статистически значим. Чтобы опровергнуть гипотезу Н0 и подтвердить гипотезу Н1 должно выполняться неравенство на уровне значимости и с (n–2) степенями свободы, где n – количество наблюдений, уровень значимости – вероятность совершить ошибку, отвергнув гипотезу Н0, когда она верна.

Для а1: Н0: а1=0, Н1: .

Рассчитаем стандартную ошибку коэффициента регрессии а1 – .

Потребуется сделать промежуточные вычисления: подставляя фактические значения хi в уравнение регрессии найдем смоделированные значения , затем вычислим разность между фактическими и смоделированными значениями, т.е. остатки , затем возведём остатки в квадрат еi2 и просуммируем; результаты представлены в расчетной таблице. Теперь подставим необходимые данные в формулу для расчёта : 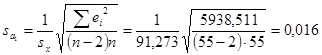иt-статистики по модулю: .

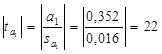Затем сравним наблюдаемое значение с табличным значением t-критерия Стьюдента. Табличное значение по таблице распределения Стьюдента на уровне значимости d=0,05 с n–2=55-2=53 степенями свободы: tтабл=2,01. Наблюдаемое значение t-статистики превышает табличное значение t-критерия: 22 > 2,01, то есть выполнено неравенство , а значит, гипотеза Н0 о случайной природе полученного коэффициента отвергается и принимается альтернативная ей гипотеза Н1, свидетельствующая в 95% случаев о статистической значимости полученного коэффициента регрессии а1. Т.о., можно считать, что взаимозаменяемость товаров подтвердилась и статистически установлена.

Для а0: Н0: а0=0, Н1: .

Рассчитаем стандартную ошибку коэффициента регрессии а0 – . Все необходимые цифры уже имеются в расчетной таблице, подставим эти данные в формулу: 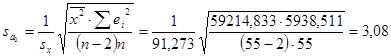, а затем рассчитаем t-статистику по модулю: .

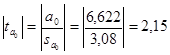Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости d=0,05 с n–2=55-2=53 степенями свободы: tтабл=2,01,где 2<ta0< 3 (tтабл > ta0) можно сделать вывод, что коэффициент регрессии а0 можно признать статистически значимым в 90% случаев.

Для rух: Н0: rух=0, Н1: .

Для этого рассчитаем стандартную ошибку коэффициента корреляции rух – : 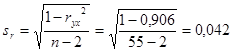иt-статистику по модулю: .

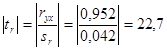Сравнивая рассчитанное значение с табличным значением t-критерия Стьюдента на уровне значимости d=0,05 с n–2=55-2=53 степенями свободы: tтабл=2,01, можно сделать вывод о статистической значимости полученного коэффициента корреляции rух в 95% случаев, предполагаемая взаимозаменяемость товаров подтвердилась.

Проверим правильность вычислений: , действительно 22»22,7.

Доверительные интервалы для параметров регрессионной модели a0 и a1

Доверительный интервал для a0 с надежностью g=1-d: . Выбрав уровень значимости d=0,05, получаем надежность g=0,95. Все необходимые цифровые значения уже рассчитаны ранее, тогда , откуда получаем (0,4312; 12,813).ыберемрительной вероятностью ров регрессионной модели

Доверительный интервал для a1 с надежностью g=1-d: . При выбранной надежности g=0,95: , откуда (0,32; 0,384).

Таким образом, с надежностью 95% можно утверждать, что истинное значение параметра a0 будет заключено в пределах от 0,4312 до 12,813, а истинное значение параметра a1 - в границах от 0,32 до 0,384.

Следует отметить, что доверительные интервалы узкие, т.к. значения стандартных ошибок и малы. А это подтверждает, что другие факторы оказывают несущественное влияние на покупательскую способность товаров. Основным фактором является выбранный фактор Х – замена растительным маслом. Значит, точность модели будет вполне приемлемой.

Оценка качества уравнения регрессии в целом

F-критерий Фишера

Выдвигается нулевая гипотеза Н0 о статистической незначимости уравнения регрессии. Альтернативная ей гипотеза Н1 о статистической значимости. Чтобы опровергнуть гипотезу Н0 и подтвердить гипотезу Н1 должно выполняться неравенство .

Рассчитаем наблюдаемое значение F-критерия (воспользуемся свойством для линейной парной регрессии): .

Табличное значение по таблице распределения Фишера на уровне значимости d=0,05 с k1=1 и k2=n–2=23-2=21 степенями свободы: Fтабл=4,03. Наблюдаемое значение F–критерия превышает табличное: 510,83 > 4,03, то есть выполнено неравенство , а значит, гипотеза Н0 о случайной природе полученного уравнения регрессии отклоняется в пользу гипотезы Н1, свидетельствующей в 95% случаев о его статистической значимости и взаимозаменяемости товаров. Уравнение по данным выборки можно признать надежным и значимым, доказывающим наличие исследуемой зависимости.

 Скачать реферат