Основы дискретной математики
Пусть V – конечное множество (множество вершин), А – множество упорядоченных пар вершин, элементы которого называются ребрами.
Тогда графом G (V, A) называется совокупность множества вершин и множества ребер. Вершины а и с соединяются ребром, если (а, с)ÌА.
Пусть дано множество вершин V и декартово произведение VхV – множество всевозможных пар вершин. Тогда графом G является подм
ножество декартового произведения.
Ребро графа G ориентировано, если порядок пары (a, b) существенен.
Ребро графа G не ориентировано, если порядок пары (a, b) несущественен.
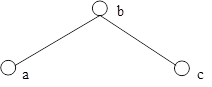
Рисунок 3.1 – Ориентированный граф
Граф называется ориентированным, если все его ребра ориентированы.
Граф G называется неориентированным, если все его ребра неориентированы.
Смешанным графом называется граф, у которого есть как ориентированные, так и неориентированные ребра.
Каждому ребру E=ía, bý можно поставить в соответствие некоторое число.
Граф G, каждому ребру которого присвоено число (например, расстояние) называется сетью.
Пусть даны a, b – вершины графа. Ребро E их соединяет. Тогда говорят, что ребро E инцидентно вершинам a и b. И обратно – вершины a и b инцидентны ребру E.
При изображении графа имеется большая свобода в размещении вершин и дуг.
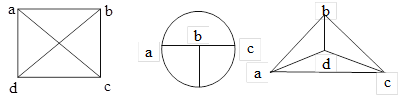
Рисунок 3.2 – Три изображения одного и того же графа
Пусть G и G1 графы, V и V1 – множества их вершин соответственно. Графы G и G1 изоморфны, если существует взаимнооднозначное соответствие между множествами их вершин V и V1 и вершины в графе G соединены ребром в том и только том случае, если соответствующие вершины соединены ребром в графе G1.
Если графы G и G1 ориентированы, то направления ребер должны соответствовать друг другу. Изоморфные графы имеют одинаковые свойства.
Вершина, не инцидентная никакому ребру, называется изолированной. Граф, состоящий из изолированных вершин, называется нуль граф. Обозначается через О.
Граф, любые две вершины которого соединены ребром, называется полным графом U=U(V).
Петлей называется ребро L=(a, a). Петля считается неориентированным ребром.
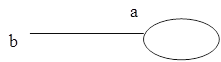
Рисунок 3.3 – Петля
Пара вершин может соединяться несколькими различными ребрами.
Пара ребер Ei Ej, ориентированная в противоположном направлении, эквивалентна одному неориентированному ребру.
Таким образом, мы можем любой неориентированный граф превратить в ориентированный. При этом количество ребер увеличивается в 2 раза.
Граф называется плоским, если может быть изображен на плоскости так, чтобы его ребра пересекались только в вершинах.
Граф назовем однородным степени k, если локальные степени во всех его вершинах равны k, т. е. ![]()
|
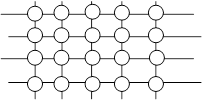
Рисунок 3.4 – Бесконечный однородный граф |
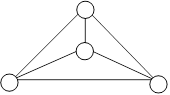
Рисунок 3.5 – Конечный однородный граф |
Граф H называется частью графа G, если подмножество вершин его V(H) содержится во множестве вершин V(G) и все ребра части графа H являются ребрами G и обозначается HÌG.
Для любой части H графа G существует дополнение ![]() , которое состоит из всех ребер графа G, не принадлежащих H.
, которое состоит из всех ребер графа G, не принадлежащих H.
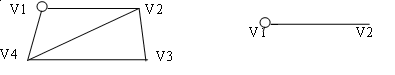
|
|
Рисунок 3.6 – Граф G Рисунок 3.7 – Часть графа G
Пусть H1 и H2 – две части графа G. Сумма этих частей H1UH2 есть часть, состоящая из ребер, принадлежащих H1 или H2. Пересечение D=H1![]() H2 – есть часть, состоящая из ребер, принадлежащих H1 и H2 одновременно. Две части не пересекаются по вершинам, если они не имеют общих вершин, и, следовательно, ребер. Части H1 и H2 не пересекаются по ребрам, если они не имеют общих ребер H1
H2 – есть часть, состоящая из ребер, принадлежащих H1 и H2 одновременно. Две части не пересекаются по вершинам, если они не имеют общих вершин, и, следовательно, ребер. Части H1 и H2 не пересекаются по ребрам, если они не имеют общих ребер H1![]() H2=0. Если H1 и H2 непересекающиеся части графа G, то их сумма называется прямой и H1UH2=G.
H2=0. Если H1 и H2 непересекающиеся части графа G, то их сумма называется прямой и H1UH2=G.
Бинарные отношения и графы
Бинарные отношения можно изобразить графом: вершины графа – элементы множества V, ребра графа соединяют вершины, которые находятся в отношении друг к другу.
Любой граф определяет бинарное отношение R на множестве вершин V, если для каждого ребра (a, b) выполняется aRb. Нельзя говорить о взаимнооднозначном соответствии между графами и бинарными отношениями. Пустому бинарному отношению соответствует нуль-граф О. Универсальному бинарному отношению отвечает полный граф U. Бинарному отношению aRb, где R – отрицание R (дополнительное бинарное отношение) отвечает граф G(R)=U(V) – G(R). Обратному бинарному отношению bR*a отвечает обратный граф G (R*), т. е. граф с измененной ориентацией ребер. Операции, которые вводятся для бинарных отношений, могут быть перенесены на графы.
Симметричное бинарное отношение: если aRb, то bRa.
Рефлексивность: бинарное отношение aRa соответствует графу с петлей в каждой вершине.
Транзитивность: если aRb и bRc, то aRc. Для графа это означает, что если существует ребро (a, b) и ребро (b, c), то существует ребро (a, c). Такой граф называется связным.
Свойство связности можно рассмотреть как бинарное отношение, которое:
а) рефлексивно: вершина а связана сама с собой;
б) симметрично: если вершина а связана с вершиной b, то и вершина b связана с вершиной a;
в) транзитивно: если вершина a связана с вершиной b, и b связана с вершиной с, то вершина a связана с вершиной c.
Отношение связности есть отношение эквивалентности, т. е. оно разбивает множество вершин на попарно непересекающиеся классы.
Так как каждое множество Vi – множество связанных вершин, а вершины из разных множеств Vi не связаны, то имеем разложение графа G на части, которые не пересекаются и каждая часть – связная.
Подграфы G(Vi) называются связными компонентами графа G.
Каждый неориентированный граф распадается единственным образом в прямую сумму всех своих связных компонент.
Покрывающие деревья
Граф, не содержащий циклов, называется ациклическим. Деревом называется связный граф, не содержащий циклов. Пусть VG – число элементов в множестве вершин, VL – число элементов множества ребер дерева.
Другие рефераты на тему «Программирование, компьютеры и кибернетика»:
Поиск рефератов
Последние рефераты раздела
- Основные этапы объектно-ориентированного проектирования
- Основные структуры языка Java
- Основные принципы разработки графического пользовательского интерфейса
- Основы дискретной математики
- Программное обеспечение системы принятия решений адаптивного робота
- Программное обеспечение
- Проблемы сохранности информации в процессе предпринимательской деятельности