Зависимость потребления бензина от количества автомобилей
Изобразим эти точки в виде точечного графика с соответствующими координатами (![]() ,
, ![]() ); для этого надо найти размах выборки по X и Y и выбрать соответствующий масштаб. Сначала находим
); для этого надо найти размах выборки по X и Y и выбрать соответствующий масштаб. Сначала находим ![]() и
и ght=23 src="images/referats/11809/image017.png">, затем размах выборки по X, которая вычисляется по формуле
![]() и в результате равна 52,61062. Аналогично
и в результате равна 52,61062. Аналогично ![]() и
и ![]() , а размах выборки поY получим равный 35,511. Глядя на размах выборок по X и по Y, выбираем масштаб диаграммы рассеивания и строим её.
, а размах выборки поY получим равный 35,511. Глядя на размах выборок по X и по Y, выбираем масштаб диаграммы рассеивания и строим её.
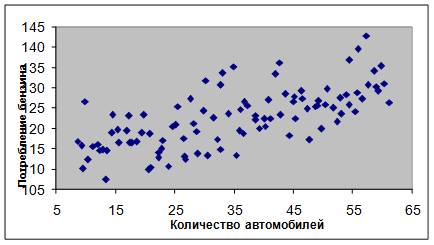
рис.1. Диаграмма рассеивания
По формуле 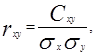 где
где 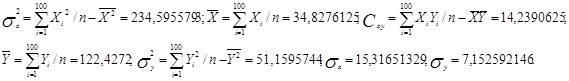
можно найти коэффициент корреляции:
![]()
Он не равен нулю, следовательно, зависимость между X и Y существует.
Построение прямой y=ax+b, наименее отклоняющейся от точек (Xi;Yi)в среднем квадратичном
Для построения прямой y = ax + b, наименее отклоняющейся от точек ![]() в среднем квадратичном, необходимо методом наименьших квадратов определить числа a, b такие, что функция двух переменных
в среднем квадратичном, необходимо методом наименьших квадратов определить числа a, b такие, что функция двух переменных ![]() принимает минимальное значение. Данная функция имеет вид:
принимает минимальное значение. Данная функция имеет вид:
![]() .
.
Зная, что необходимым условием минимума функции является равенство нулю ее первых частных производных, имеем следующую систему для нахождения значений ![]() :
:
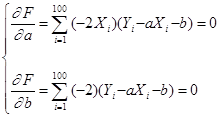 ,
, 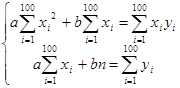
Данная система может быть представлена в виде:
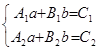 ,
,
где 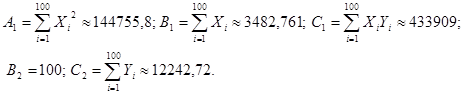
В результате получим что:
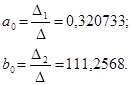
Докажем теперь, что в точке ![]() функция
функция ![]() имеет минимум. Достаточным условием существования экстремума функции двух переменных является следующее неравенство:
имеет минимум. Достаточным условием существования экстремума функции двух переменных является следующее неравенство:
![]()
![]() .
.
Для доказательства введем следующие обозначения:
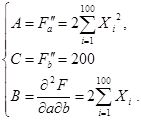
Составим дискриминант ![]() . Тогда, если
. Тогда, если ![]() , то функция имеет в точке экстремум, а именно минимум при А>0 (или С>0). Из системы видно, что эти условия выполняются:
, то функция имеет в точке экстремум, а именно минимум при А>0 (или С>0). Из системы видно, что эти условия выполняются: ![]() =
= ![]() , С=200>0.
, С=200>0.
То есть точка ![]() действительно является точкой минимума.
действительно является точкой минимума.
Следовательно, функция ![]() при данных значениях
при данных значениях ![]() имеет следующий график:
имеет следующий график:
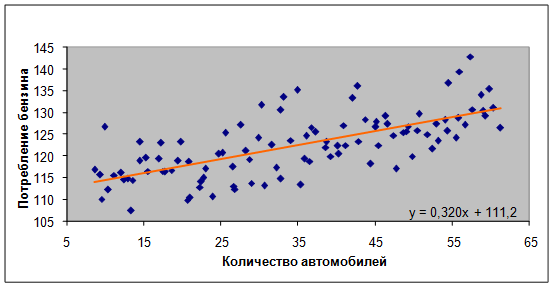
рис.2. График уравнения линейной регрессии
Построение кривой y=px2+qx+r, наименее отклоняющейся от точек (Xi;Yi) в среднем квадратичном
Для построения кривой ![]() , наименее отклоняющейся от точек
, наименее отклоняющейся от точек ![]() в среднем квадратичном, необходимо методом наименьших квадратов определить числа
в среднем квадратичном, необходимо методом наименьших квадратов определить числа ![]() ,
, ![]() и
и ![]() такие, что функция трех переменных
такие, что функция трех переменных ![]() принимает минимальное значение. Данная функция имеет вид:
принимает минимальное значение. Данная функция имеет вид:
![]()
Аналогично нахождению значений ![]() для прямой
для прямой ![]() составляем систему трех линейных уравнений, которая является необходимым условием минимума функции:
составляем систему трех линейных уравнений, которая является необходимым условием минимума функции:
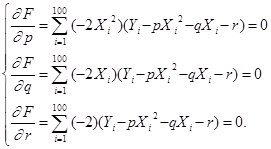
![]()
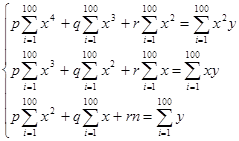
Данная система является системой линейных однородных уравнений. Решая эту систему методом Крамера и зная, что:
![]()
![]()
составляем определители, состоящие из коэффициентов при ![]() и столбца свободных членов.
и столбца свободных членов.
Значения ![]() находим делением соответствующих определителей.
находим делением соответствующих определителей.
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
Докажем теперь, что в точке ![]() функция
функция ![]() имеет минимум. Достаточным условием существования минимума функции трех переменных является следующее неравенство:
имеет минимум. Достаточным условием существования минимума функции трех переменных является следующее неравенство:
d![]() .
.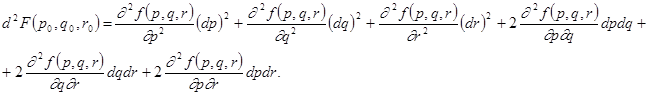
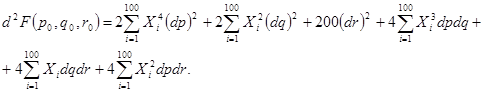
Получаем следующее уравнение:
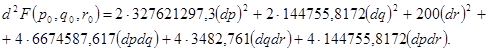
Воспользуемся критерием Сильвестра, т.е. найдем миноры 1-ого, 2-ого и 3-ого порядков и докажем, что они положительные.
![]() =
=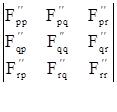
![]()
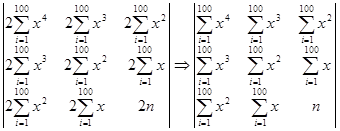 =
=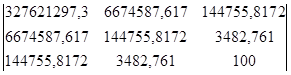
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
