Дифференциальные уравнения

А-1 * А * Х = А-1 * Н

Но А-1 * А = Е (Е- единичная матрица), а ЕХ = Х, поэтому

Х = А-1 * Н(2)

Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.

Пусть имеем невырожденную матрицу

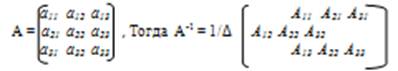
где Аij (i=1,2,

3; j=1,2,3) – алгебраическое дополнение элемента аij в определителе матрицы А, которое является произведением (- 1)ij на минор (определитель) второго- порядка, полученный вычеркиванием i-строки и j-столбца в определителе матрицы А.

Вычислим определитель Δ и алгебраические дополнения Аij элементов матрицы А.

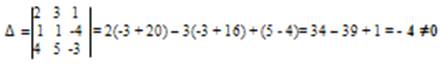
Следовательно матрица А имеет обратную матрицу А-1.

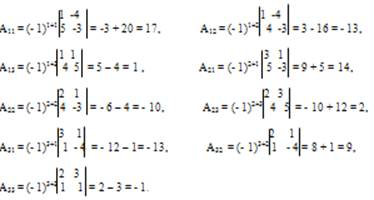
Тогда

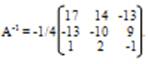
По формуле (2) находим решение данной системы уравнений в матричной форме:

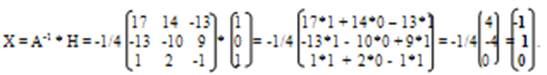
Отсюда

х = - 1; у = 1; z = 0.

Задача №4

Вычислить пределы.

Решение

а) Подстановка предельного значения аргумента х = 3 приводит к неопределенному выражению вида .

Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим на множитель (х – 3). Такое сокращение здесь возможно, так как множитель (х – 3) отличен от нуля при х →3:

б) При х→∞ выражение дает неопределенность вида . Для устранения этой неопределенности применим правило Лопиталя. Для разыскания предела отношения двух функций, бесконечно больших при х→∞, можно рассматривать отношение их производных .Если оно стремится к пределу (конечному или бесконечному), то к тому же пределу стремится и отношение .

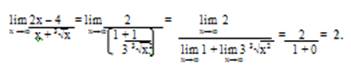
в) Обозначим arctg 3х = у. Тогда 3х = tg у и у→0 при х→0. Применяя свойства пределов и формулу первого замечательного предела lim sin α/ α = 1, имеем:

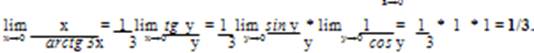
г)При х→∞ выражение является неопределенностью вида 1∞. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой при х→∞ величины и применим формулу второго замечательного предела:

Тогда имеем:

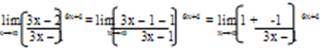
Пусть 3х – 1 = - у . Тогда 6х + 4 = - 2у + 6 и у→ -∞ при х→∞. Переходя к переменной у, получим:

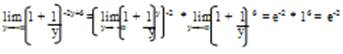
Задача №5

Найти производные функций:

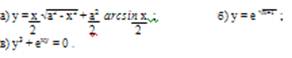
Решение

а) Последовательно применяя правило дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

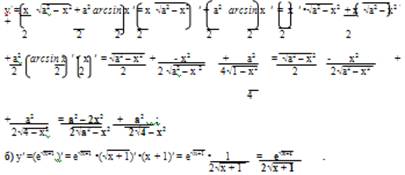
в) В данном случае функциональная зависимость задана в неявном виде. Для нахождения производной у′ нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно у′ .

3у2у′ + еху (у + ху′) = 0, 3у2у′ + уеху + хеху у′ = 0,

Из последующего уравнения находим у′:

у′ (3у2 + хеху) + уеху = 0,

Задача №6

Исследовать функцию методами дифференциального исчисления и построить ее график. Исследование функции рекомендуется проверить по следующей схеме:

1) найти область определения функции;

2) исследовать функцию на непрерывность;

3) определить, является ли данная функция четной, нечетной;

4) найти интервалы возрастания и убывания функции и точки ее экстремума;

5) найти интервалы выпуклости и вогнутости графика функции и точки перегиба;

6) найти асимптоты графика функции.

Решение

1. Функция определена при всех значениях аргумента х.

2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т.е. на интервале (- ∞; ∞).

3. Для установления четности и нечетности функции проверим выполнимость равенств f(- х) = f( х) (тогда f( х) – четная функция) или f(-x) = - f(х) (для нечетной функции) для любых х и – х из области определения функции:

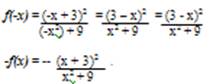
Следовательно, f(-х) ≠ f(x) и f(-х) ≠ -f(х), то есть данная функция не является ни четной, ни нечетной.

4. Для исследования функции на экстремум найдем ее первую производную:

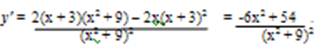
у′ = 0 при х1 = - 3, х2 = 3. Тем самым имеем две критические точки, обе принадлежать области определения функции.

Разобьем числовую ось на три интервала: (- ∞; - 3), (- 3; 3), (3; ∞).

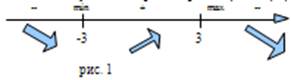
В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает, во втором интервале – положительна и данная функция возрастает. При переходе через точку х = -3 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум:

уmin = у(-3) = 0

Значит, А(-3;0) – точка минимума.

При переходе через точку х = 3 первая производная меняет свой знак с плюса на минус, поэтому в этой точке функция имеет максимум:

уmax = у(3) = 2

Значит, В(3;2) – точка максимума.

На рис. 1 знаками +, - указаны интервалы знакопостоянства производной у′, а стрелками – возрастание и убывание исследуемой функции.

5. Для определения точек перегиба графика и интервалов выпуклости и вогнутости кривой найдем вторую производную:

у′′ = 0 при х1 = 0, х2 = - 3√3 , х3 = 3√3.

Разобьем числовую ось на четыре интервалы: (-∞;-3√3), (-3√3 ;0), (0;3√3), (3√3 ; ∞).

 Скачать реферат