Оптимальные методы в совершенствовании планирования и управления производством

Bj - необходимый объем продукции j-го вида;

Ds - общий объем ограниченных ресурсов s-го вида;

- объем производства j-ой продукции на i-м предприятии при k-ом варианте его развития;

- величина расхода s-x ресурсов на i-м предприятии при k-ом варианте его раз

вития;

- искомые величины (булевы переменные), означающие интенсивности способов (вариантов) производства;

- значение оценок переменных в целевой функции модели (величина капиталовложений на i-м предприятии при k-ом варианте его развития, приведенные затраты и т. д.).

В принятых обозначениях задача сводится к следующему: найти значения переменных , при которых минимизируется величина целевой функции

(1)

и выполняются условия

(2)

- все предприятия отрасли должны произвести не меньше заданного объема по каждому виду продукции;

(3)

- все предприятия отрасли могут использовать дефицитные ресурсы в рамках имеющихся возможностей или лимитов;

(4)

- условие целочисленности переменных величин. Переменная величина равна единице, если данный вариант развития i-го предприятия используется в оптимальном плане, или равен нулю, если он не используется.

В задачах оптимального отраслевого регулирования существует большое множество вариантов плана (векторов ) удовлетворяющих условиям (1) – (4). Во время решения задачи на ЭВМ из этого множества выбирается такой вектор интенсивности , при котором минимизируется значение целевой функции (1). Эти значения будут оптимальным планом при принятых условиях. Подстановка этого вектора в систему (1) – (4) позволит определить конкретные показатели плана.

При решении конкретных задач в систему (1) – (4) могут вводиться дополнительные ограничения и переменные величины. Например, ограничения на мощность отдельных предприятий или группы предприятий; ограничения и переменные, отражаемые возможность взаимозамещаемости отдельных ресурсов или продукции и т. д.

Рассмотрим данную модель на условном примере:

Пусть требуется произвести два вида продукции в объеме 20 и 10 ед. соответственно. Они могут производиться на двух предприятиях. Использование лимитированного ресурса ограничено 100 ед. По каждому предприятию разработаны два варианта их развития, отличающиеся объемом производства продукции, величиной расхода ресурсов и приведенными затратами на весь выпуск. Данные приведены в таблице 1.

Таблица 1

Развернутая запись задачи будет иметь вид:

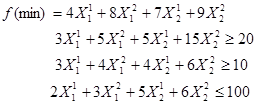
Результат решения данной задачи:

Х* = (0;1;0;1)

f(Х*) = 17(8+9)

Прогнозируемый объем производства двух видов продукции необходимо разместить на двух предприятиях отрасли в соответствии с полученными значениями искомых переменных величин в оптимальном плане:

 Скачать реферат