Дискретно-аналоговое представление

Рисунок 6

Известно, что в этом случае в соответствии с теоремой

В.А. Котельникова возможно разложение первичного сигнала в ряд:

, (16)

где - частота опроса. В точках 4 src="images/referats/8197/image057.png">интерполирующая функция равна:

. (17)

Сопоставим этот результат с выражением для идеальной интерполирующей функции:

. (18)

Чтобы эти формулы совпали, необходимо чтобы при , а в случае , т. е. чтобы корреляционная функция имела вид:

. (19)

Такой функцией корреляции обладает сигнал с прямоугольным спектром, а условие при приводит к требованию, чтобы частота опроса .

Это соотношение не может быть использовано на практике по следующим причинам:

1. Сигнала с идеальным прямоугольным спектром не существует.

2. Число выборок .

На практике при представлении регулярными выборками частота опроса выбирается исходя из соотношения

æ, (20)

где определяется формой спектра сигнала, а æ – коэффициент запаса, зависящий от вида интерполирующих полиномов и требуемых значений показателя верности.

4. Интерполяция алгебраическими полиномами

цифровой кодирование алгебраический полином

Как было показано выше, для первичных сигналов с разными корреляционными функциями необходимо использовать разные интерполирующие функции. Такой подход не приемлем для практики, т.к. требует выполнения большого объема предварительных работ для определения вида интерполирующих функций. Для преодоления этих затруднений возможны два пути:

1. Использование для группы сигналов с близкими корреляционными функциями интерполирующей функции одного вида.

2. Применение в качестве интерполирующих функций хорошо программируемых функций с выбором частоты опроса, обеспечивающих во всех случаях требуемую верность.

Второй путь наиболее прост, но приводит к завышенным частотам опроса и, следовательно, к увеличению загрузки радиолинии. Наиболее рациональным является комбинированное использование обоих путей.

Во многих случаях в качестве интерполирующих путей используются алгебраические полиномы низких степеней, в частности полиномы Лагранжа. Интерполирующая функция по Лагранжу записывается в следующем виде:

(21)

где - символ произведения, в котором отсутствуют сомножители при . Нетрудно убедиться, что при и при .

При интерполяции по Лагранжу требуется определенным образом выбрать интервал обработки .

1) Число точек опроса n четное (рисунок 7).

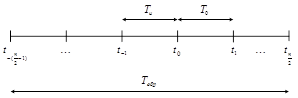
Рисунок 7

2) Число точек опроса n нечетное (рисунок 8).

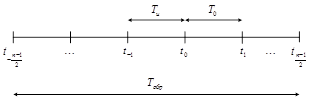
Рисунок 8

Запишем момент времени, в котором ищется интерполяционная оценка в виде

, (22)

где - точка отсчета, - период опроса, - безразмерное время, которое может непрерывно изменяться в пределах

, при (23)

, при , (24)

На практике интерполяция по Лагранжу используется при n = 1, 2, 3:

1. Ступенчатая интерполяция (полиномы нулевой степени ) (рисунок 9).

В этом случае n = 1 и для интерполяции используется лишь одна выборка

, , и .

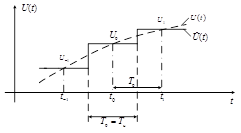
Рисунок 9

2. Линейная интерполяция (полиномы первой степени) (рисунок 10).

При этом , , и интерполирующие функции имеют вид

, .

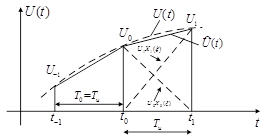
Рисунок 10

3. Квадратичная интерполяция (квадратичная интерполяция) (рисунок 11).

При этом , , и интерполирующие функции имеют вид

, , .

 Скачать реферат