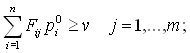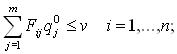Математические методы экономики
Очевидно, что аналогичные распределения можно провести и для конкурента В, который должен рассмотреть все свои стратегии, выделяя для каждой из них максимальные значения проигрыша: ![]() (последняя строка матрицы).
(последняя строка матрицы).
Из всех значений ![]() находят минимальное:
находят минимальное:
=129 height=37 src="images/referats/5477/image075.png">,
которое дает минимаксный выигрыш или минимакс.
Такая ![]() -стратегия - минимаксная, придерживаясь которой сторона В гарантировано, что в любом случае проиграет не больше
-стратегия - минимаксная, придерживаясь которой сторона В гарантировано, что в любом случае проиграет не больше ![]() . Поэтому
. Поэтому ![]() называют верхней ценой игры.
называют верхней ценой игры.
Если ![]() , то число С называют чистой ценой игры или седловой точкой.
, то число С называют чистой ценой игры или седловой точкой.
Для игры с седловой точкой нахождение решения состоит в выборе пары максиминной и минимаксной стратегий, которые являются оптимальными, так как любое отклонение от этих стратегий приводит к уменьшению выигрыша первого игрока и увеличению проигрыша второго игрока по сравнению с ценой игры С.
Однако не все матрицы имеют седловую точку. Тогда решение находят, применяя смешанные стратегии, то есть чередуя случайным образом несколько чистых стратегий (гибкая тактика).
Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называют смешанной стратегией данного игрока.
Из этого определения следует, что сумма компонент этого вектора равна единице, а сами компоненты не отрицательны.
Обычно смешанную стратегию первого игрока обозначают как вектор
![]() , а второго игрока - как вектор
, а второго игрока - как вектор ![]() , где
, где 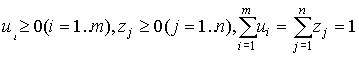 . (5.1.1).
. (5.1.1).
Если u° - оптимальная стратегия первого игрока, z° - оптимальная стратегия второго игрока, то число 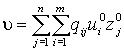 - называют ценой игры.
- называют ценой игры.
Для того чтобы число ![]() - было ценой игры, а u° и z° — оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
- было ценой игры, а u° и z° — оптимальными стратегиями, необходимо и достаточно выполнение неравенств:
![]() , (5.1.2)
, (5.1.2)
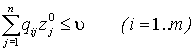 . (5.1.3)
. (5.1.3)
Если один из игроков применяет оптимальную смешанную стратегию, то его выигрыш равен цене игры и вне зависимости от того, с какими частотами будет применять второй игрок стратегии, вошедшие в оптимальную, в том числе и чистые стратегии
Внимание к седловым точкам в теории игр традиционно. Объясняется это недоверием к максимину, как к принципу оптимального выбора в том случае, когда нет седловой точки. Поэтому естественно стремление заполнить промежуток между максимином и минимаксом путем применения смешанных стратегий.
Однако, не следует забывать, что: 1) применение смешанных стратегий рисковано, когда игра не повторяется; 2) если игра повторяется, надо иметь уверенность, что у противника нет информации о конкретных решениях другого игрока; 3) противник не обязан применять смешанные стратегии, равно как и стремиться к цели, противоположной цели другого игрока.
Обозначим смешанную стратегию первого игрока p = {pi}, ![]() где pi - вероятность применения i-й стратегии,
где pi - вероятность применения i-й стратегии, 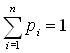 ,
, ![]() . Пусть смешанная стратегия второго игрока
. Пусть смешанная стратегия второго игрока ![]() ,
, ![]() , qj - вероятность применения j-й стратегии,
, qj - вероятность применения j-й стратегии, 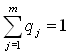 ,
, ![]() . Р и Q определяют математическое ожидание платежа:
. Р и Q определяют математическое ожидание платежа:
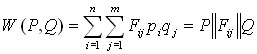 .
.
Теорема фон Неймана. Любая матричная игра имеет седловую точку в смешанных стратегиях.
Доказательство. Множества M и N ограничены и замкнуты, так как ![]() ,
, ![]() , а функция W непрерывна по P и Q . W линейна по P при фиксированных Q, следовательно, вогнута по P при фиксированных Q. Аналогично W выпукла по Q при фиксированных P. M и N выпуклы.
, а функция W непрерывна по P и Q . W линейна по P при фиксированных Q, следовательно, вогнута по P при фиксированных Q. Аналогично W выпукла по Q при фиксированных P. M и N выпуклы.
Действительно, рассмотрим такие ![]() и
и ![]() , что
, что 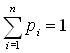 ,
, 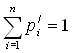 , тогда
, тогда ![]() ,
, ![]() .
.
Складывая, получим ![]() .
.
Кроме того, ![]() .
.
Следовательно, при![]() и
и ![]()
![]()
тоже смешанная стратегия.
Применяя фундаментальную теорему, получим то, что требуется доказать:
![]() .
.
Опираясь на доказанную теорему, можно быть уверенным, что решение игры в смешанных стратегиях всегда существует (если только вообще их можно применять). В теории игр доказывается теорема, указывающая на эквивалентность решения матричной игры в смешанных стратегиях и двойственной задачи линейного программирования.
Пусть Po и Qo оптимальные смешанные стратегии, v - цена игры, тогда
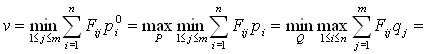
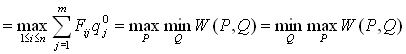 .
.
Из теорема следует, что
|
|
(4) |
|
|
(5) |
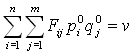 .
.
Обозначим ![]() .
.
Поделим (4) на v , получим
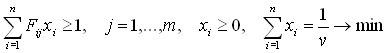 .
.
Другие рефераты на тему «Экономико-математическое моделирование»:
Поиск рефератов
Последние рефераты раздела
- Выборочные исследования в эконометрике
- Временные характеристики и функция времени. Графическое представление частотных характеристик
- Автоматизированный априорный анализ статистической совокупности в среде MS Excel
- Биматричные игры. Поиск равновесных ситуаций
- Анализ рядов распределения
- Анализ состояния финансовых рынков на основе методов нелинейной динамики
- Безработица - основные определения и измерение. Потоки, запасы, утечки, инъекции в модели