Классический метод расчета переходных процессов в линейных цепях

Содержание

1. Возникновение переходных процессов и законы коммутации

2. Способы получение характеристического уравнения

3. Особенности переходных процессов в цепях с одним реактивным элементом

4. Переходные процессы в цепях с двумя разнородными реактивными элементами

5. Временные характеристики цепей

6. Расчет реакции линейной цепи на входное воздейств

ие произвольного вида с применением временных характеристик цепи

Список используемых источников

1. Возникновение переходных процессов и законы коммутации

Для изучения темы реферата необходимо знать расчет установившихся режимов, т.е. таких, когда все токи и напряжения либо постоянные, либо периодически повторяющиеся функции времени, но в любой схеме могут происходить подключения и отключения ветвей (происходит коммутация). Обозначают коммутацию: . В линейных цепях коммутация считается идеальной, т.е.:

1) ключ представляет собой либо разрыв, либо провод;

2) длительность перехода из одного состояния в другое равна нулю. Момент времени сразу после коммутации обозначают либо , а момент времени непосредственно перед коммутацией соответственно обозначают , . После коммутации цепь стремится под действием источников схемы прийти к новому установившемуся режиму, но для этого ей требуется время. Процессы, происходящие в цепи после коммутации, называются переходными процессами.

Почему этот переход не может произойти мгновенно? Дело в том, что в цепи имеются элементы L и C, в которых запасается определенная величина энергии WL=L2/2 и WC=Cu2/2 соответственно. В новом установившемся режиме будет другой запас энергии, и, т.к. скорость изменения энергии есть подводимая к элементу мощность, получается, что требуется конечное время на изменение этого запаса энергии (т.к. источников бесконечной мощности в реальной цепи нет). Из выражения для WL и WC и того факта, что в цепях не развивается бесконечная мощность, вытекают два фундаментальных условия, без которых невозможно рассчитать ни один переходной процесс – это законы коммутации.

Получим их:

,

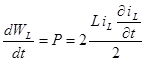т.к. P, L - конечное число, L - конечное число, то - скачка быть не может. Отсюда вытекает один из законов коммутации: ток в индуктивности не может измениться скачком, поэтому при коммутации: . Дифференцируя dWC/dt, приходим ко 2-ому закону коммутации: напряжение на ёмкости не может измениться скачком, поэтому при коммутации: . Т.к. = LL, , то можно использовать и такие функции: , .

Про остальные величины, в том числе и про скорость изменения любых токов и напряжений при коммутации заранее ничего не известно и их приходится рассчитывать. Т.к. и форма изменения токов и напряжений неизвестна, приходится использовать самые общие выражения: , . Тогда уравнения, описывающие цепь после коммутации, оказываются дифференциальными. В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов.

2 Способы получение характеристического уравнения

Классический метод

Классический метод основан на решении ЛДУ методом вариации произвольных постоянных. Любая система ЛДУ может быть сведена к одному уравнению n –ого порядка. В цепях по схеме после коммутации порядок определяется так: n = n L + n C – nОК – nОС , где n L – число L; n C – число C; nОК – число особых контуров, т.е. таких, которые состоят только из емкостей и источников ЭДС; nОС – число особых сечений (в простейшем случае, это узлы схемы, к которым подключены только ветви с источником тока или с индуктивностями).

Решение уравнения представляют в виде суммы частного решения неоднородного уравнения (ЛНДУ) и общего решения линейного однородного дифференциального уравнения (ЛОДУ). Частное решение определяется видом правой части уравнения. В цепях в правой части уравнения стоят источники энергии схемы после коммутации. Физический смысл частного решения уравнения в цепях – это новый установившийся режим, к которому будет стремиться схема после коммутации под действием источников. Поэтому частное решение ЛНДУ называют принужденной составляющей режима. Общее решение ЛОДУ физического смысла не имеет. В противоположность принужденной составляющей, его называют свободной составляющей переходного процесса. Свободная составляющая записывается в виде суммы слагаемых, число и вид которых определяются корнями характеристического уравнения.

После записи решения необходимо рассчитать произвольные постоянные, вошедшие в выражение общего решения. Это можно сделать, если известны начальные условия. Начальные условия – это значения искомой функции времени и необходимого числа её производных по времени в начале переходного процесса, т.е. при t=0.

Все начальные условия делят на две группы:

- независимые начальные условия, это L(0) и uC(0), которые находятся по законам коммутации, с помощью вычисленных ранее L(0-) и uC(0-) в схеме до коммутации;

- все остальные начальные условия – зависимые. Их приходится искать из цепи после коммутации в переходном режиме по законам Кирхгофа для мгновенных значений токов и напряжений при t=0 с помощью независимых начальных условий. Имея необходимое число начальных условий и рассматривая решение и его производные по времени в момент , получают систему линейных алгебраических уравнений (СЛАУ) из которой находят произвольные постоянные.

В соответствии с изложенным, порядок расчета переходного процесса классическим методом может быть таким:

1) рассматривают установившийся режим схемы до коммутации и находят L(0-) и uC (0-);

 Скачать реферат