Звук - физика, химия, биология

Найдем проекции натяжения на оси x и u (обозначим их Tx и Tu):

где α – угол касательной к кривой u(x,t) с осью x. На участок (x1, x2) действуют силы натяжения, внешние силы и сил

ы инерции. Сумма проекции всех сил на ось x должна быть равна нулю (мы рассматриваем только поперечные колебания). Так как силы инерции и внешние силы по предположению направлены вдоль оси u, то

(1)

Отсюда в силу произвольности x1 и x2 следует, что натяжение не зависит от x, т. е. для всех значений x и t

(2)

Перейдем к выводу уравнения поперечных колебаний струны. Воспользуемся вторым законом Ньютона. Составляющая количества движения участка струны (x1, x2) по оси u равна

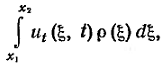
где ρ – линейная плотность струны. Приравняем изменение количества движения за промежуток времени ∆t = t2 - t1

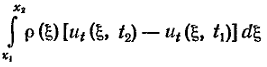
импульсу действующих сил, складывающихся из натяжения

в точках x1 и x2 и внешней силы, которую будем считать непрерывно распределенной с плотностью (нагрузкой) F(x, t), рассчитанной на единицу длины. В результате получим уравнение поперечных колебаний элемента струны в интегральной форме

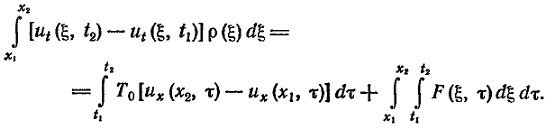(3)

Для перехода к дифференциальному уравнению предположим существование и непрерывность вторых производных от u(x, t). Тогда фотмула (3) после двукратного применения теоремы о среднем примет вид

где

Сократим на ∆x∆t и переходя к пределу при x2→x1, t2→t1, получим дифференциальное уравнение поперечных колебаний струны

(4)

В случае постоянной плотности ρ = const этому уравнению обычно придают вид

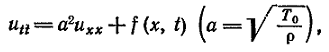(5)

где

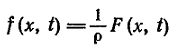(6)

есть плотность силы, отнесенная к единице массы. При отсутствии внешней силы получим однородное уравнение

или

описывающее свободные колебания струны. Это уравнение является простейшим примером уравнения гиперболического типа.

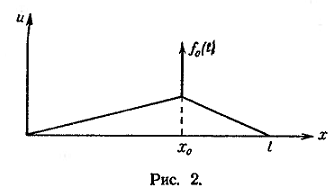
Если в точке x0(x1<x0<x2) приложена сосредоточенная сила f0(t) (рис. 2), то уравнение (3) запишется так:

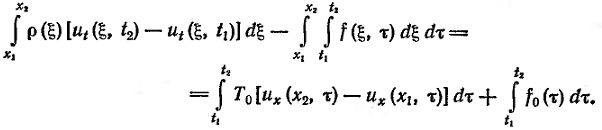
Поскольку скорости точек струны ограничены, то при x1→x0 и x2→x0 интегралы в левой части этого равенства стремятся к нулю, и равенство (3) принимает вид

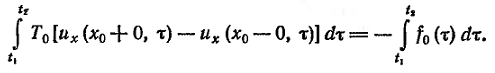(7)

Пользуясь теоремой о среднем, сокращая обе части равенства на ∆t и переходя к пределу при t2→t1 получим:

Отсюда видно, что в точке приложения сосредоточенной силы первые производные претерпевают разрыв и дифференциальное уравнение теряет смысл. В этой точке должны выполняться два условия сопряжения

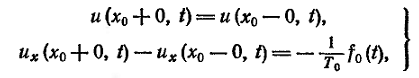(8)

второе из которых выражает непрерывность струны, второе определяет величину излома струны в точке x0, зависящую от f0(t) и натяжения T0.

Теперь рассмотрим задачу о поперечных колебаниях струны, закрепленной на концах. В этой задаче u(x, t) дает отклонение струны от оси x. Если концы струны 0 ≤ x ≤ l закреплены, то должны выполняться «граничные условия»

u(0, t) = 0, u(l, t) = 0.

Так как процесс колебания струны зависит от её начальной формы и распределения скоростей, то следует задать «начальные условия»:

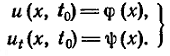
Таким образом, дополнительные условия состоят из граничных и начальных условий, где φ(x) и ψ(x) – заданные функции точки.

Эти условия вполне определяют решение уравнения колебания струны

2.2 Метод Фурье для уравнения колебаний ограниченной струны.

Начальные условия:

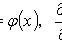
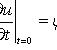
Граничные условия:

Решение:

где

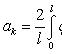
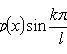
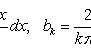
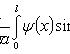
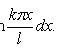
Каждая функция представляет собой гармоническое колебание с частотой

ωn = kπa / l . Амплитуда колебаний для разных точек разная. На концах струна неподвижна. Все точки струны одновременно достигают своего максимального отклонения в ту или другую сторону и одновременно проходят положения равновесия. Такие колебания называются стоячими волнами. Неподвижные точки называются узлами стоячей волны. Посредине между узлами расположены точки, в которых отклонения достигают максимума. Эти точки назывются пучностями стоячей волны.

Т. е. колебание конечной струны представляет собой бесконечную сумму стоячих волн, каждая из которых имеет постоянную частоту колебания и изменяющуюся по длине струны амплитуду. В -й стоячей волне имеется пучностей и узлов.

 Скачать реферат