Особенности изучения темы "Поверхности вращения второго порядка" в школьном курсе математики

Однополостный гиперболоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy - гипербола.

Двуполо

стный гиперболоид

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.

Двуполостный гиперболоид изображен на рисунке 4.

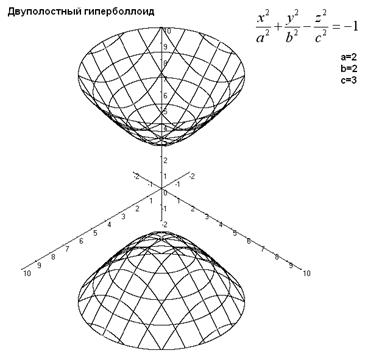
Рис.4

Свойства двуполостного гиперболоида

Двуполостный гиперболоид - неограниченная поверхность, поскольку из его уравнения следует, что

Двуполостный гиперболоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при |z|>c получается эллипс, при |z|=c - точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, - гипербола.

Коническая поверхность

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, c > 0, называется конической поверхностью. Коническая поверхность изображена на рисунке 5.

Свойства конической поверхности

Коническая поверхность - неограниченная поверхность, поскольку из её уравнения следует, что z - любое число.

Коническая поверхность обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

В сечении конической поверхности плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy - прямые.

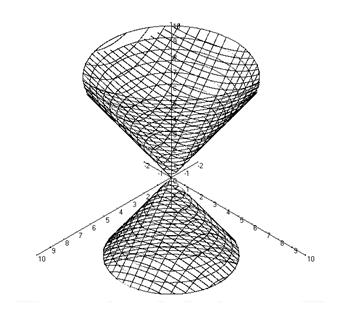
Рис. 5

Цилиндрическая поверхность

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, называется цилиндрической поверхностью. Цилиндрическая поверхность изображена на рисунке 6.

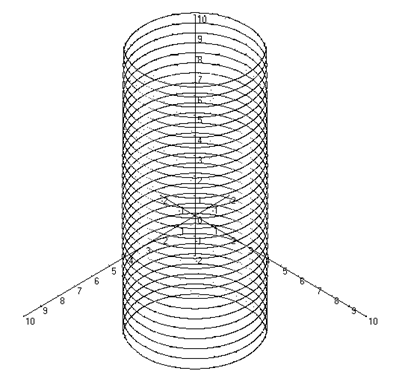
Рис. 6

Свойства цилиндрической поверхности

Цилиндрическая поверхность - неограниченная поверхность.

Цилиндрическая поверхность обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

В сечении цилиндрической поверхности плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy - прямые.

Поверхностью вращения второго порядка называется поверхность заданная линией второго порядка, которая вращается вокруг одной из осей координат и в сечении плоскостью параллельной одной из координатных плоскостей получается окружность. В уравнении такой поверхности существует особенность: два знаменателя в сумме дробей равны.

1.3 Способы получения поверхностей вращения второго порядка

1.3.1 Геометрический способ

Пусть дана кривая l, которая лежит в плоскости XOY и имеет уравнение ; (рис.7). Найдём уравнение поверхности, которая получается при вращении кривой l вокруг оси ОХ (рис.8).

Очевидно, что точка М с координатами (x, y, z), где принадлежит искомой поверхности тогда и только тогда, когда , таким образом уравнение поверхности, полученной вращением кривой вокруг оси ОХ имеет вид: , . Это уравнение получено из уравнения кривой l следующим образом: обе части уравнения возводятся в квадрат и y2 заменяется на y2+ z2.

При вращении кривой или прямой вокруг одной из координатных осей можно получить поверхность вращения.

Для этого необходимо уравнение прямой или кривой сначала возвести в квадрат, а затем при их вращении вокруг оси OY x2 заменяется на x2+y2, при вращении вокруг оси ОХ y2 заменяется на y2+ z2.

Эллипсоид вращения

Поверхность, которая получается при вращении эллипса вокруг одной из осей, называется эллипсоидом вращения. Пусть в плоскости XOY эллипс задан уравнением: .

Составим уравнение поверхности, полученное вращением эллипса вокруг оси ОХ. Для этого в уравнении эллипса y2 заменим на y2+ z2. После замены получим: (I).

Это уравнение называется уравнением эллипсоида. При a >b уравнение (I) определяет эллипсоид вращения, вытянутый вдоль оси ОХ (приложение 1 рис.9), при a < b - эллипсоид вращения сжатый вдоль оси ОХ (приложение 1 рис.10), при a = b уравнение определяет сферу (приложение 1 рис.11).

Однополостный и двуполостный гиперболоиды вращения

Пусть в плоскости ХОУ дана гипербола, заданная уравнением . При вращении гиперболы вокруг одной из её осей получится поверхность вращения, называемая гиперболоидом вращения.

При вращении гиперболы вокруг её действительной оси (ОХ), получается двуполостный гиперболоид, чтобы получить его уравнение необходимо (достаточно) в уравнении гиперболы y2 заменяется на y2+ z2. После замены получим: . Двуполостный гиперболоид изображен в приложении 1 рис.12.

При вращении гиперболы вокруг её мнимой оси (ОУ), получается однополостный гиперболоид. Для получения уравнения поверхности однополостного гиперболоида нужно в уравнении гиперболы заменить x2 на x2+z2 после замены получим . Однополостный гиперболоид изображен в приложении 1 рис 13.