Методика обучения студентов педагогических вузов теме: "Сложное отношение точек. Полный четырехвершинник"

воспитательная: воспитывать положительное отношение к процессу обучения, уважение к сверстникам и преподавателю.

Тип занятия: лекция.

Структура занятия:

1.Организационный момент (2 мин).

2.Мотивация к изучению темы (3 мин).

3.Изложение нового материала (80 мин).

4.Итог занятия (5 мин).

Ход занятия

1.Организационный момент.

- преподаватель здоровается и отмеча

ет отсутствующих студентов;

- сообщается тема занятия, его цель: Сегодня мы продолжаем изучение «Проективной геометрии», рассмотрим тему «Сложное отношение четырех точек прямой», которая будет читаться в течении одной лекции. На этой лекции мы познакомимся с понятием сложного отношения четырех точек прямой, а так же узнаем основные свойства сложного отношения четырех точек прямой, сложное отношение четырех прямых пучка.

2.Мотивация к изучению темы.

Начнём с того, что необходимость изучения темы «Сложное отношение точек» проективной геометрии вытекает из её роли в дальнейшей педагогической деятельности.

Например: Часто предлагаемые на школьных олимпиадах задачи довольно трудно решить, зная только школьный курс геометрии, но при более глубоком изучении геометрии в вузе решение таких задач становится гораздо легче. Так например, некоторые задачи носят проективный характер, и при их решении необходимы знания отношения четырех точек прямой, а также четырех прямых пучка.

Всё это требует знания различных свойств сложного отношения точек. И вы, как будущие учителя, всё это должны знать, так как, с одной стороны, изучение этих вопросов углубляет его понимание элементарной геометрии, а с другой стороны, расширяет кругозор студентов как будущих учителей математики.

3. Изложение нового материала осуществляется с помощью традиционных методов обучения и слайдов по теме «Сложное отношение точек», которые отражаются мультимедиа-проектором и содержат основной материал лекции.

§ 1. Сложное отношение четырех точек (четырех прямых)

1. Определение сложного отношения четырех точек прямой

Пусть точки лежат на одной прямой и заданы своими координатами: в некотором репере .

Определение. Сложным отношением упорядоченной четверки точек называется число равное

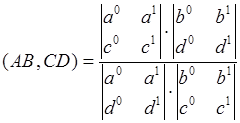. (1)

Коротко можно записать так 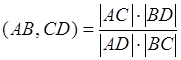, где определитель составленный из координат точек и .

Сложное отношение точек не зависит от выбора проективного репера. Если – собственные точки прямой, то выполняется равенство:

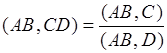. (2)

Пусть точки имеют координаты: , , . Поскольку проективные координаты определяются с точностью до проективного множества, то можно считать, что эти точки имеют координаты:

, , , . (*)

Где 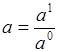, ,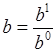,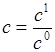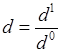. Поскольку, сложное отношение точек не зависит от выбора репера, то в качестве репера можно выбрать репер , тогда будут являться аффинными координатами на данной прямой.

Найдем простое отношение (используя определение простого отношения): , .

Найдем сложное отношение по формуле (1), используя координаты (*):

.

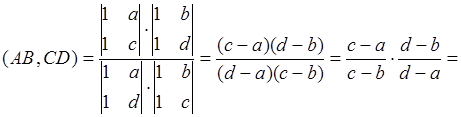
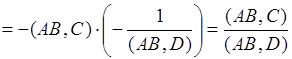Замечание 1. Несобственная точка делит любой отрезок прямой в отношении , то есть .

Замечание 2. Если выбрать в качестве репера , то в этом репере точка будет иметь координаты: . Зная сложное отношение точек , всегда можно найти расположение точки на прямой. В этом случае .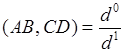

Значит, если , то .

2. Свойства сложного отношения четырех точек

10: Сложное отношение точек не изменится, если поменять местами пару точек: .

Доказательство: 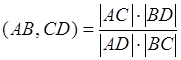, 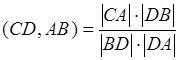. Учитывая, что получим, что . Свойство доказано.

20: Сложное отношение точек меняет свое значение на обратное, при перестановке точек внутри одной пары: .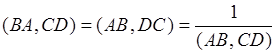

Доказательство: 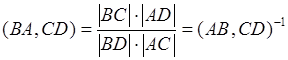, 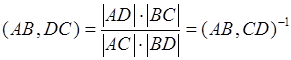. Свойство доказано.