Методика обучения студентов педагогических вузов теме: "Сложное отношение точек. Полный четырехвершинник"

4. Сложное отношение точек заданных своими координатами на проективной плоскости

Как найти сложное отношение четырех точек прямой , зная их координаты , , , относительно репера на плоскости?

Прямая не проходит по крайней мере через одну из точек . Для определенности будем считать, что (рис. 3).

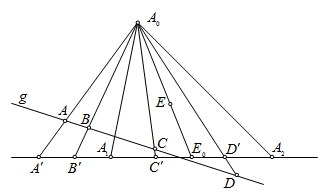
Рис.3

Рассмотрим перспективное отображение с помощью пучка прямых П(). Имеем:

. (5)

В репере на прямой имеем координаты точек:

.

Поэтому

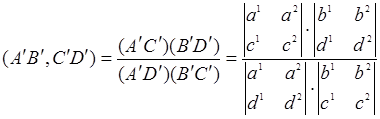
и, учитывая равенство (5),

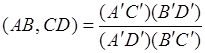. (6)

Аналогичные выражения получим, если прямая не проходит через вершину или координатного треугольника, проектируя точки прямой на из или на и из .

На проективной плоскости возьмем репер и произвольную точку . Пусть – проекции точек и на прямую из центра . Мы знаем, что в репере на прямой точка имеет координаты и, следовательно, по формуле (2) 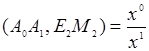при условии, что , то есть . Аналогичные выражения получим и для других отношений между координатами точки . Поэтому справедлива

Теорема 4. Если точка имеет координаты относительно репера проективной плоскости, то отношение 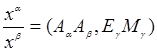равно сложному отношению четырех точек: двух вершин , и проекций , на прямую точек и из третьей вершины координатного треугольника (при условии, что , т. е. ) [3].

4.Итог занятия.

Итак, сегодня мы познакомились с понятием сложного отношения четырех точек прямой, изучили свойства сложного отношения, рассмотрели сложное отношение четырех прямых пучка.

– Как обозначается сложное отношение четырех точек прямой?

Возможный вариант ответа: (AB,CD).

– Какие свойства сложного отношения точек сегодня были изучены?

– Каким отношением связанно сложное отношение четырех точек прямой и отношение трех точек прямой?

– При обозначении сложного отношения точек важен порядок записи точек?

Лекция № 2

Тема: Полный четырехвершинник

Цель: обучающая: ввести определение гармонической четверки точек, изучить теорему о свойствах полного четырехвершинника;

развивающая: развивать память, логическое мышление, умение анализировать, выделять закономерности, обобщать, способность быстро ориентироваться в ситуации;

воспитательная: воспитывать положительное отношение к процессу обучения, уважение к сверстникам и преподавателю.

Тип занятия: лекция.

Структура занятия:

1.Организационный момент (2 мин).

2.Изложение нового материала (85 мин).

3.Итог занятия (3 мин).

Ход занятия

1.Организационный момент.

- преподаватель здоровается и отмечает отсутствующих студентов;

- сообщается тема занятия, его цель: На этой лекции мы познакомимся с понятием гармонической четверки точек, изучим теорему о свойствах полного четырехвершинника.

2. Изложение нового материала осуществляется с помощью традиционных методов обучения и слайдов по теме «Полный четырехвершинник», которые отражаются мультимедиа-проектором и содержат основной материал лекции.

§2. Гармонические четверки. Полный четырехвершинник

Четверка точек прямой называется гармонической, если . Говорят также, что точки и гармонически сопряжены относительно точек и или что пары , и , гармонически разделяют одна другую. Точку называют при этом четвертой гармонической к упорядоченной тройке точек , , .