Границы применимости закона Дарси. Нелинейные законы фильтрации

На основе анализа данных, приведенных в табл. 1.1, можно сделать следующие выводы.

1. Несмотря на отмеченные недостатки результатов Н. Н. Павловского, есть основания для их сопоставления с соответствующими результатами трубной гидравлики. Важно подчеркнуть, что критические значения числа Рейнольдса, подсчитанные по формуле (1.11), намного меньше тех, которые в трубной гидравлике соответству

ют переходу ламинарного течения в турбулентное. Это служит одним из доводов в пользу того, что причины нарушения закона Дарси при высоких скоростях фильтрации (увеличение влияния сил инерции по мере увеличения ) не следует связывать с турбулизацией течения. Отсутствие турбулентности при нарушении закона Дарси было доказано также прямыми опытами, изложенными Г. Шнебели.

Формулы Фэнчера, Льюиса и Бернса получены формальным введением в выражение для числа Рейнольдса эффективного диаметра в качестве характерного размера пористой среды, они не сопоставимы с результатами трубной гидравлики, дают слишком узкий диапазон изменения значений (см. графу 4 табл. 1.1), мало обоснованы.

2. Во все другие формулы табл. 1.1 (графы 5-9) в качестве характерного размера входят величины, пропорциональные (где k-коэффициент проницаемости породы), методы определения которых хорошо известны. Формулы этой группы не имеют принципиальных преимуществ и одинаково удобны для практического использования. Для этих формул характерно то, что все они приводят к очень широким диапазонам изменения для различных пористых сред. И это представляется вполне естественным ввиду разнообразия свойств испытанных пористых сред. Кроме того, это свидетельствует о том, что ни в одну из предложенных формул для определения не входит полный набор параметров, позволяющий характеризовать сложную структуру пористых сред, использования для этой цели коэффициентов пористости проницаемости явно недостаточно.

Вместе с тем, широкий диапазон изменения значений можно разбить на сравнительно узкие интервалы, соответствующие различным группам образцов пористых сред. Это облегчает указание возможной верхней границы справедливости закона Дарси при движении флюида в какой-либо пористой среде.

Результаты такого разбиения для формулы В. Н. Щелкачева (см. табл. 1.1, первая строка, пятая графа) приведены в табл. 1.2.

Итак, при значениях числа Рейнольдса линейный закон Дарси перестает быть справедливым. Первое обобщение закона Дарси на случай больших основанное на опытных данных, было выполнено Дюпюи, который сформулировал двучленный закон.

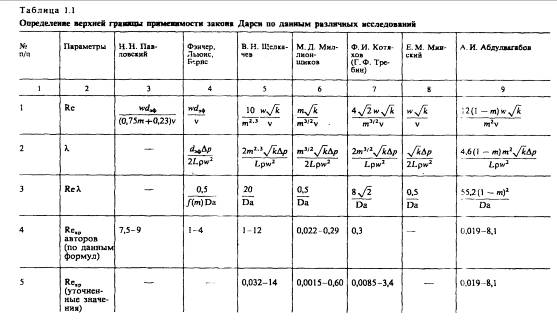
Таблица 1.2

Интервалы критических значений для образцов пористых сред

фильтрации, носящий имя австрийского исследователя Ф. Форхгеймера, независимо установившего его несколько позднее. В принятых сейчас обозначениях это соотношение можно представить (для простейшего случая прямолинейно-параллельного течения без учета силы тяжести) в следующем виде:

(1.14)

где b - дополнительная константа пористой среды, определяемая экспериментально.

Первое слагаемое в правой части (1.14) учитывает потери давления вследствие вязкости жидкости, второе - инерционную составляющую сопротивления движению жидкости, связанную с криволинейностью и извилистостью поровых каналов. Из (1.14) следует, что при малых скоростях фильтрации квадратом скорости w2 можно пренебречь, и градиент давления будет зависеть только от первого слагаемого, т.е. движение будет безынерционным, соответствующим закону Дарси. При больших скоростях фильтрации силы инерции становятся существенными и будут сопоставимы или даже преобладать над силами вязкости.

Хорошая согласованность соотношения (1.14) с данными промысловых и экспериментальных наблюдений была установлена в много численных работах советских и зарубежных исследователей. Это свидетельствует о том, что данное соотношение представляет нечто большее, чем простую эмпирическую формулу, поскольку оно хорошо выполняется даже для весьма больших значений скорости фильтрации. Физический смысл этого заключается в том, что при больших скоростях быстропеременное движение в порах вследствие «извилистости» поровых каналов сопряжено с появлением значительных инерционных составляющих гидравлического сопротивления. С увеличением числа Рейнольдса квадратичный член в выражении (1.14) оказывается преобладающим, силы вязкости пренебрежимо малы по сравнению с силамиинерции, и (1.14) сводится тогда к квадратичному закону фильтрации, предложенному А. А. раснопольским. Он справедлив в средах, состоящих из частиц достаточно крупных размеров.

2. Отклонения от закона Дарси при малых скоростях фильтрации

В опытах, проведенных в конце прошлого века с тонкозернистыми грунтами при малых скоростях, было обнаружено увеличение скорости фильтрации с ростом градиента давления более быстрое, что это дает линейный закон Дарси. Однако объяснение этого факта не приводилось.

Начиная с 50-х годов XX в. появилось большое число теоретических и экспериментальных работ, подтвердивших нарушения закона Дарси в области малых скоростей. Это явление заметнее всего при движении воды в глинах, но наблюдается также и при фильтрации в песках и песчаниках не только воды, но и нефтей. При этом во всех экспериментах обнаруживалась существенная нелинейность закона фильтрации при малых скоростях.

 Скачать реферат