Методы, способы, приемы решения физических задач

r1+r2=R12 (R13+R23) / (R12+ R13 + R23).

Аналогично для точек 1 и 3 и для точек 2 и 3:

r1+r3=R13 (R12+R23) / (R12+ R13 + R23).

r2+r3=R23 (R12+R13) / (R12+ R13 + R23).

Сложив левые и правые части этих уравнений и разделив полученные суммы на 2, получим:

r1+r2+r3= (R12R13 +R12 R23 + R13 R23) /) / (R12 + R13 + R23).

После преобразований получим:

r1=R12R13/ (R12+R13+R23);

r2=R12R23/ (R12+R13+R23);

r3=R13R23/ (R12+R13+R23).

Аналогично получаются формулы для обратного преобразования:

R12= (r1r2+r1r3+r2r3) / r3;

R13= (r1r2+r1r3+r2r3) / r2;

R23= (r1r2+r1r3+r2r3) / r1.

Задача: Определите сопротивление цепи АВ (рис.31. а), если R1=R5= 1 Oм; R2=R6=2Oм; R3=R7=3 Oм; R4=R8 =4 Oм.

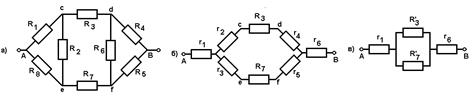
рис.31

Преобразуем "треугольники" R1 R2 R8 R4 R5 R6 в эквивалентные "звёзды", тогда схема примет вид, изображённый на рис.35, б. Сопротивления r1, r2, r3, … r6 рассчитаем по формулам: r1 = R1 R8/ (R1 + R2 + R8) = 4/7 Ом;

r2 = R1 R2/ (R1 + R2 + R8) = 2/7 Ом; r3 = R2 R8/ (R1 + R2 + R8) = 8/7 Ом;

r4=R4R6/ (R4+R5+R6) =8/7Ом; r5 = R5 R6/ (R4 + R5 + R6) = 2/7 Ом;

r6 = R4 R5/ (R4 + R5 + R6) = 4/7 Ом;

Схема, изображённая на рис.31, в является эквивалентной схеме на рис.31, б. Здесь R’3 = r2 + R3 + r4 = 31/7 Ом; R’7 = r3 + R7 + r5 = 31/7 Ом, R’3 = R’7. Общее сопротивление цепи

Rобщ = r1 + R’3/2 + r6 = 47/14 Ом.

Задача: Определить общее сопротивление неуравновешенного моста (рис.32, а), если R1 = 1,0 Oм; R2 = 1,6 Oм; R3 = 2,0 Oм; R4 = 1,2 Oм; R5 = 2,0 Oм.

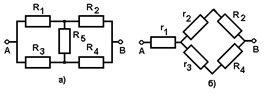
рис.32

Если преобразовать "треугольник" из резисторов R1, R3, R5 в эквивалентную "звезду", то получится простая схема (рис.32, б). Рассчитаем сопротивления r1, r2 и r3 по формулам:

r1 = R1R3/ (R1 + R3 + R5) = 0,4 Ом; r2 = R1R5/ (R1 + R3 + R5) = 0,4 Ом; r3 = R3R5/ (R1 + R3 + R5) = 0,8 Ом;

Общее сопротивление цепи

Rобщ = r1 + (r2 + R2) (r3 +R4) / (r2 + R2 + r3 + R4) = 1,4 Ом.

Векторный метод решения задач

Этот метод используется в случае, если при сложении векторов получается замкнутый треугольник. Это может быть треугольник скоростей, сил, импульсов, напряжённостей электрических и индукций магнитных полей.

Задача: Мальчик и девочка решили попасть из пункта А в пункт В, расположенные на противоположных берегах реки, скорость течения которой u. Мальчик плывёт так, чтобы сразу оказаться в пункте В. Девочка направляет скорость своего плавания поперёк скорости течения реки и, чтобы попасть в пункт В, должна пройти по противоположному берегу то расстояние, на которое её снесёт течением. С какой скоростью должна перемещаться девочка по берегу, чтобы оказаться в пункте В одновременно с мальчиком? Скорости и мальчика, и девочки относительно воды одинаковы и равны V.

При решении используем закон сложения скоростей, согласно которому скорость тела относительно неподвижной системы отсчёта равна сумме скорости относительно подвижной системы и скорости самой подвижной системы. На рис.33, а показана скорость мальчика V1 относительно берегов, которая получается путём сложения скорости мальчика относительно воды V и скорости течения реки u. Модуль скорости V1 определим по теореме Пифагора: V1= (V2 - u2) 1/2.

Время, за которое мальчик сумеет переплыть реку по прямой АВ, определим по формуле: t1 = L/V1, L - ширина реки.

На рис.33, б показана скорость девочки V2 относительно берегов реки, которая также равна сумме векторов скоростей девочки относительно воды V и течения реки u. Однако по модулю она равна V2= (V2+u2) 1/2.

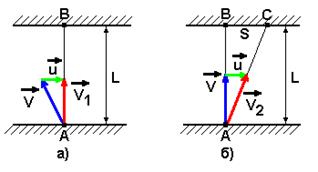
рис.33

Время, которое потребуется девочке, чтобы переплыть реку по прямой АС равно:

t2=L/V,

т.к. вдоль прямой АВ она плывёт со скоростью V. Поскольку V > V1, то t2 < t1 на величину

Δt = t1 - t2 = L (1/V1 - 1/V).

Девочка приплывает в пункт С и, чтобы попасть в пункт В вместе с мальчиком ей требуется перемещаться по прямой ВС со скоростью V ‘ = S/ Δt, где S - длина прямой ВС, представляющая собой расстояние, на которое сносит девочку течение реки. Из подобия векторного треугольника и треугольника АВС (рис.33, б) составим пропорцию S/L = u/V, откуда найдём S:

S = Lu/V.

Скорость перемещения девочки по прямой ВС будет равна: V ‘= S/Δt= Lu/VΔt или после подстановки значения Δt и V1:

V ‘=u/V (1/V1-1/V) =u/V [1/ (V2 - u2) 1/2 - 1/V].

Задача: (стр.17) можно решить не только координатным методом, но и векторным.

На шарик действуют силы: mg - сила тяжести, FA - архимедова сила, T - сила натяжения нити и FE - сила, действующая на заряд шарика со стороны электрического поля (рис.9).

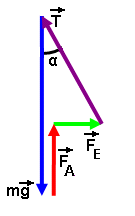
рис.34

Произведя сложение векторов этих сил, получим векторный треугольник со сторонами (mg - FA), FE и Т.

По условию равновесия сумма векторов сил должна быть равна нулю, поэтому конец вектора Т должен совпасть с началом вектора mg (рис.34). Так как сила натяжения направлена вдоль нити, а сила тяжести вертикально вниз, то между ними будет угол α. Угол между векторами mg и FE прямой. Отношение противолежащего катета к прилежащему для угла α равно тангенсу этого угла: tgα=FE/ (mg-FA).

Метод решения обратной задачи

Многие физические явления, изучаемые в школьном курсе физики, рассматриваются в идеальных условиях.

При рассмотрении механических явлений часто пренебрегают сопротивлением среды, трением, рассеянием энергии, поэтому такие явления носят обратимый характер. Для таких случаев направление прямого процесса можно заменить обратным процессом.

Задача:

С какого расстояния S от центра полусферы радиуса R =1,35 м, с какой скоростью и под каким углом β нужно бросить маленькую шайбу (из положения 1), чтобы она, попав на полусферу, остановилась на её вершине (положение 2) (рис.35, а)? Трением шайбы о полусферу и сопротивлением воздуха пренебречь. Ускорение свободного падения считать равным 10 м/с2.

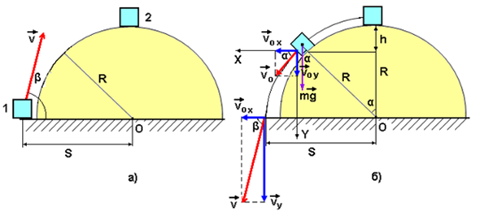
рис.35

Сформулируем обратную задачу: на каком расстоянии S от центра полусферы, с какой скоростью V и под каким углом β упадёт шайба, скатывающаяся с вершины полусферы радиуса R (рис.35, б)? Трением шайбы о поверхность полусферы и сопротивлением воздуха пренебречь.

Определим, с какой скоростью V0, под каким углом α к горизонту и с какой высоты от уровня основания полусферы (R cosα) отрывается шайба от поверхности полусферы. Точка отрыва лежит ниже вершины на расстоянии равном h, поэтому скорость шайбы в момент отрыва определится по формуле: V0 = (2gh) 1/2.

В момент отрыва шайбы от поверхности сферы сила реакции опоры становится равной нулю, сила трения равна нулю по условию, поэтому единственной силой, действующей на шайбу в этот момент, является сила тяжести. Точка отрыва шайбы является точкой перехода её траектории с дуги окружности радиуса R на параболическую кривую. Составляющая силы тяжести, действующая вдоль радиуса, является силой, сообщающей шайбе центростремительное ускорение, поэтому скорость шайбы в момент отрыва можно определить по второму закону Ньютона: mg cos α = m V02/R, откуда