Методы, способы, приемы решения физических задач

Далее решаем систему из третьего и последнего уравнений. Приравняв левые части этих равенств, и сократив на S, получим выражение: 2/t1-1/t2=1/ t3.

Откуда t3= t1t2/ (2t2-t1).

Задача: Посередине откачанной и запаянной с обоих концов трубки длиной L, расположенной горизонтально, находится столбик ртути длиной h. Если трубку поставить вертикально, то столбик ртути сместится на расстояние ра

вное d. До какого давления была откачана трубка? Плотность ртути ρ.

Процесс перевода трубки из горизонтального положения в вертикальное (рис.13) можно считать изотермическим, и, следовательно, к состояниям газа в обеих частях трубки применить закон Бойля-Мариотта.

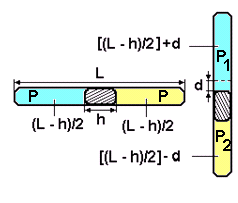
рис.13

Поскольку площадь поперечного сечения трубки остаётся постоянной, то объёмы частей трубки, занятые газом, пропорциональны их длинам. Тогда для газа в верхней части трубки закон Бойля-Мариотта запишется так:

Р (L - h) /2 = P1 [ (L - h) /2 + d];

а для газа в нижней части трубки - Р (L - h) /2 = P2 [ (L - h) /2 - d]. Здесь Р1 и Р2 - давления газа в верхней и нижней частях трубки соответственно, которые связаны между собой соотношением: Р2-Р1=ρgh.

Решая полученную систему из трех уравнений относительно давления газа Р в обеих частях трубки при её горизонтальном положении, получаем

Р = ρgh [ (L - h) 2 - 4d2] (L - h) d.

Система уравнений законов сохранения.

При столкновении тел (ударе) всегда выполняется закон сохранения импульса, вне зависимости от вида удара упругого или неупругого. Закон сохранения механической энергии выполняется при абсолютно упругом ударе, при неупругом - часть механической энергии переходит во внутреннюю энергию.

При движении тел по замкнутым криволинейным траекториям (окружность, эллипс) в отсутствии силы сопротивления выполняются законы сохранения момента импульса и энергии.

Задача: Два шарика массами m и 3m висят, соприкасаясь, на длинных нерастяжимых нитях. Шарик меньшей массы вместе с нитью, на которой он подвешен, отклоняют на угол 90о и шарик отпускают. Определить отношение импульсов (р1/р2) шариков после столкновения. Удар считать абсолютно упругим.

Пусть первый шарик массой m в самый последний момент до удара со вторым шариком массой 3m имеет импульс р. После удара импульс первого шарика р1 направлен противоположно, потому что его масса меньше массы второго. Второй шарик имеет импульс р2 (рис.14).

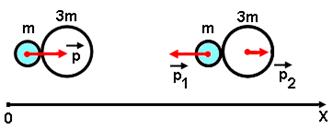
рис.14

Запишем выражение закона сохранения импульсов шариков в проекциях импульсов на координатную ось 0Х: р=р2-р1.

Это уравнение содержит два неизвестных р1 и р2. Запишем второе уравнение, в которое входили бы эти же неизвестные. Это уравнение закона сохранения энергии (в данном случае кинетической энергии), которая сохраняется, вследствие абсолютно упругого удара: р2/2mр12/ 2m+ р22/ 6m.

Здесь используется формула, связывающая кинетическую энергию с импульсом. Приведём систему из двух уравнений к следующему виду:

р + р1 =р2

р2-р12=р22/ 3.

После деления второго уравнения системы на первое получим выражение: р - р1 = р2/3, которое решаем совместно с уравнением р=р2-р1. Получаем соотношение: р2-р1=р2/3+р1.

Разделив обе части равенства на р2, получим искомое соотношение импульсов 1 - (р1/р2) = 1/3 + (р1/р2).

Откуда р1/р2 = 1/3.

Задача: Космический корабль обращается вокруг Луны по круговой орбите, радиус которой равен трём радиусам Луны (R = 3Rл). Какую минимальную скорость нужно сообщить спускаемому аппарату, чтобы он прилунился на противоположной стороне Луны? (рис.15)

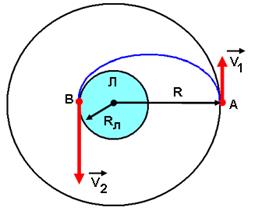
рис.15

Сначала определим скорость V0 космического корабля при его движении вокруг Луны по круговой орбите радиуса R, используя второй закон Ньютона: G Mm/R2 = mV02,где М - масса Луны, m - масса космического корабля, G - гравитационная постоянная.

Отсюда V0= (GM/R) 1/2= (GM/3Rл) 1/2.

Подставив в формулу значения гравитационной постоянной, массы и радиуса Луны, взятые из справочника (G = 6,672 10-11 Hм2/кг2, М = 7,35 1022кг, Rл = 1737 км) получаем значение этой скорости: V0 = 970 м/с.

Чтобы прилуниться в точке В, космический аппарат должен двигаться по эллиптической орбите (рис.15), а для этого его скорость должна измениться и стать равной V1. При движении по этой траектории выполняются законы сохранения момента импульса и энергии:

mV1R=mV2Rл;

mV12/2-GMm/R=mV22/2-GMm/Rл.

Спускаемый аппарат обладает как кинетической энергией, вследствие движения, так и потенциальной энергией, вследствие гравитационного взаимодействия с Луной.

Видоизменим полученную систему уравнений, учитывая, что R = 3Rл.

3V1 = V2;

V12-2GM/3Rл=V22-2GM/Rл.

Решая полученную систему уравнений относительно V1, получаем выражение для скорости, которая обеспечит начало движения спускаемого аппарата по эллиптической орбите V1= (GM/6Rл) 1/2.

Подставив в формулу значения гравитационной постоянной, массы и радиуса Луны получаем значение этой скорости: V1 = 686 м/с.

Сравнение скоростей V0 и V1 показывает, что V1 < V0, следовательно, чтобы изменить скорость спускаемого аппарата от V0 до V1, ему нужно сообщить скорость V в направлении, противоположном вектору скорости V0, равную

V = V0 - V1 = 970 - 686 = 284 м/с

Для сообщения этой скорости спускаемому аппарату, его нужно развернуть двигательной установкой по движению корабля и включить её.

Метод отрицательных масс

Этот метод используется при решении задач на определение положения центра масс фигуры, имеющей удалённые из неё участки. В этом случае массу удалённого участка считают отрицательной, а силу тяжести этого участка (-mg) направляют вверх. В дальнейшем используют условие равновесия тела, находящегося под действием системы параллельных сил. Здесь используется понятие момента силы.

Задача: Определить координату ХС центра масс однородного цилиндра радиуса R, в котором высверлено сквозное цилиндрическое отверстие радиуса r, ось которого параллельна оси цилиндра и находится от неё на расстоянии d.

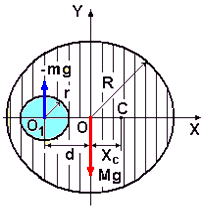
рис.16

Изобразим поперечное сечение цилиндра с высверленным в нём цилиндрическим отверстием. Сечение проводим через середину длины цилинра. Центр масс (точка С) (рис.16) находится на оси Х, проходящей через точки О и О1. После удаления цилиндрической части радиуса r он смещается вправо от оси основного цилиндра. На рисунке указываем силы тяжестей сплошного цилиндра Mg и удалённого цилиндра (-mg). Под действием этих сил цилиндр остаётся в равновесии, если ось вращения проходит через центр масс. Условие равновесия тела, имеющего ось вращения заключается в равенстве нулю суммы моментов сил, приложенных к телу, относительно этой оси.

Условие равновесия будет иметь вид: Mg XC - mg (d + XC) = 0.

Массы М и m определим по формулам:

М=ρV=ρπR2L; m=ρ π r2L,