Методы, способы, приемы решения физических задач

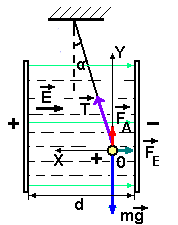
рис.9

Изобразим шарик в положении равновесия, в котором нить образует угол α с вертикалью. Электрическое поле, возникающее между пластинами при подаче на них напряжения U, считаем однородным. Силовые линии такого поля параллельны друг другу и направлены перпендикулярно поверхностям пластин от пластин

ы с большим потенциалом (+) к пластине с меньшим потенциалом (-). Вектор напряжённости Е параллелен силовым линиям, а его величина определяется соотношением: Е = U/εd,

где ε - диэлектрическая проницаемость керосина.

На шарик действуют силы: mg - сила тяжести, FA-архимедова сила, T-сила натяжения нити и FE - сила, действующая на заряд шарика со стороны электрического поля (рис.9).

Запишем условия равновесия шарика в виде проекций сил на координатные оси ОХ: Тsinα-FE = 0;

OY: Tcosα+FA - mg = 0.

Представим эти уравнения в виде:

Т sin α = FE;

Tcos α = mg - FA.

Поделив левые и правые части этих уравнений, получим соотношение

tgα=FE/ (mg-FA).

Из этого уравнения выразим силу FE, FE= (mg-FA) tgα.

По законам электростатики эта сила определяется по формуле:

FE=Eq=Uq/εd,

где q - заряд шарика.

Приравняв правые части последних двух уравнений получим уравнение, из которого можно найти заряд шарика: Uq/εd= (mg-FA) tgα. Подставим в уравнение выражения для силы тяжести и силы Архимеда, связав их с плотностями алюминия и керосина, соответственно:

mg=ρaVg= (4/3) πr3ρag,

FA=ρkVg= (4/3) πr3ρkg.

Получим уравнение:

Uq/εd= (4/3) π r3g (ρa - ρk) tg α,

из которого найдём заряд шарика

q=4πr3gεd (ρa - ρk) tg α / 3U.

Метод решения задач переходом в систему отсчёта, связанную с одним из движущихся тел

Переход в систему отсчета, связанную с одним из движущихся тел, заключается в том, что это тело в его системе отсчёта становится неподвижным, а его скорость и ускорение, направленные противоположно, передаются второму телу. Пусть в неподвижной системе отсчёта два тела А и В имеют скорости VA и VB, векторы которых направлены как показано на рис.10, а.

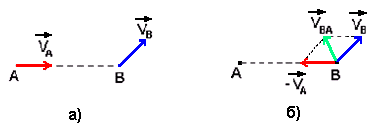
рис.10

Скорость VBA тела В в системе отсчёта, связанной с телом А, определится как векторная сумма векторов VB и (-VA), а скорость тела А в этой системе становится нулевой (рис.10, б).

Задача: Спортсмены бегут колонной длины L со скоростью v. Навстречу бежит тренер со скоростью u, причём u <v (рис.11, а). Каждый спортсмен, поравнявшись с тренером, разворачивается и начинает бежать назад с той же по модулю скоростью v. Какова будет длина колонны, когда все спортсмены развернуться.

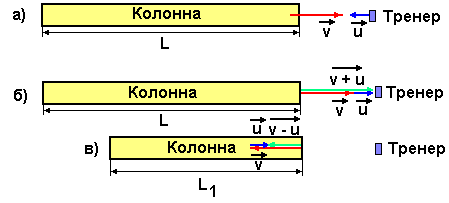
рис.11

Задачу решаем в системе отсчёта, связанной с тренером. В этой системе отсчёта тренер неподвижен, а спортсмены при беге навстречу тренеру имеют скорость равную сумме скоростей (v + u) (рис.11, б), а при беге от тренера (v-u) (рис.11, в). Время, за которое все спортсмены, поравнявшись с тренером, повернут назад равно: t = L/ (v + u).

Расстояние, на которое удалится первый, поравнявшийся с тренером спортсмен, за это время и будет определять новую длину колонны.

Спортсмены бегут от тренера со скоростью (v - u), поэтому первый спортсмен за время t убежит на расстояние L1, которое определится по формуле:

L1 = (v - u) t = L (v - u) / (v + u).

Это и будет новой длиной колонны, она станет короче.

Задача: Два автомобиля выезжают одновременно из пунктов А и В, расположенных на расстоянии L друг от друга. Первый автомобиль А едет по прямой дороге, направленной под углом α к прямой АВ со скоростью VA, а второй В - по прямой дороге, составляющей с прямой АВ угол β, со скоростью VB (рис.12, а). Определить, каким будет минимальное расстояние между автомобилями при их движении?

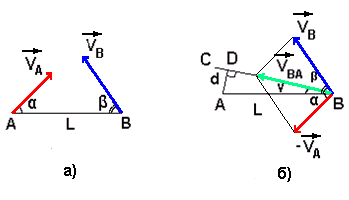
рис.12

Изобразим движение автомобиля В в системе отсчёта, связанной с автомобилем А (рис.12, б).

В этой системе отсчёта автомобиль А неподвижен, а автомобиль В движется со скоростью VBA вдоль прямой ВС. Кратчайшее расстояние от неподвижного в этой системе отсчёта автомобиля А до прямой ВС определится длиной перпендикуляра АD, которая и даст значение минимального расстояния d между автомобилями. Это расстояние определится из прямоугольного треугольника ADB по формуле: d = L sin γ.

Угол γ определяется из векторного треугольника скоростей использованием теоремы синусов:

VA / sin (β - γ) = VB / sin (α +γ)

VA (sinα cosγ + sinγ cosα) = VB (sinβ cosγ - sinγ cosβ)

Разделив обе части равенства на cosγ, получим

VA (sinα+tgγ cosα) =VB (sinβ - tgγ cosβ).

Отсюда tgγ = (VBsinβ - VAsinα) / (VAcosα+VB cosβ),

γ = arc tg (VB sinβ-VA sinα) / (VA cosα + VB cosβ),

Подставив в выражение для d значение угла γ, получаем значение минимального расстояния между автомобилями

d = L sin arc tg (VB sinβ - VA sinα) / (VA cosα + VB cosβ).

При решении таким методом задач на столкновение тел вектор скорости VBA должен быть направлен точно на тело А, а угол γ должен быть равен нулю.

Метод составления системы уравнений

Система идентичных уравнений.

Метод используется при решении тех задач, в которых рассматривается одно и то же физическое явление, происходящее при разных условиях, отражённых в данных задачи. При составлении уравнений необходимо проанализировать, какие физические величины, описывающие это явление, остаются одинаковыми.

Задача: Эскалатор (движущаяся лестница) спускает идущего по нему пассажира за время t1, а движущегося по нему в два раза быстрее за время t2. За какое время эскалатор спускает стоящего на нём пассажира?

В этой задаче одинаковыми являются длина эскалатора S и скорость его движения u. Скорость первого пассажира в неподвижной системе отсчёта по закону сложения скоростей складывается из скорости пассажира относительно эскалатора v и скорости самого эскалатора u: v1=v+u, её также можно определить по определению скорости v1=S/t1. Тогда для скорости движения первого пассажира получим соотношение: S/t1=v+u.

Аналогично для скорости движения второго пассажира, который движется относительно эскалатора со скоростью 2v: S/t2=2v+u.

Для третьего пассажира уравнение скорости движения будет иметь вид: S/t3=u.

В системе трёх уравнений четыре неизвестных: S, v, u и искомое t3, поэтому необходимо понизить число неизвестных. Для исключения неизвестной скорости v, вычтем второе уравнение из первого уравнения, умноженного на 2. В результате чего получим уравнение: S (2/t1-1/t2) =u.