Методика решения иррациональных уравнений и неравенств в школьном курсе математики

Необходимо запомнить формулу . Уравнение теперь легко решается

.

Ответ. .

Теперь посмотрим "обратное" преобразование.

Пример 7. Решить уравнение .

Решение. Сейчас настало время задуматься о безопасности формулы

.

Нетрудно видеть, что ее левая и правая части имеют разные области определения и что это равенство верно лишь при условии . Поэтому исходное уравнение равносильно системе

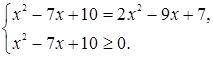
Ответ. .

II. Следующее преобразование, которое должно явиться предметом заботы для каждого, кто решает иррациональные уравнения, определяется формулой

.

Если пользоваться этой формулой слева направо, расширяется ОДЗ и можно приобрести посторонние решения. Действительно, в левой части обе функции и должны быть неотрицательны; а в правой неотрицательным должно быть их произведение.

Замечание. При возведении уравнения в квадрат учащиеся нередко в уравнении типа (1) из Примера 5 производят перемножение подкоренных выражений, т.е. вместо такого уравнения пишут уравнение

.

Такое "склеивание" не приводит к ошибкам, поскольку такое уравнение является следствием уравнения (1). Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения. Поэтому в рассмотренном выше примере можно было сначала перенести один из радикалов в правую часть уравнения, т.е. уединить один радикал. Тогда в левой части уравнения останется один радикал, и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональное выражение.

Пример 8. Решить уравнение

.

Решение. Уединив первый радикал, получаем уравнение

,

равносильное исходному.

Возводя обе части этого уравнения в квадрат, получаем уравнение

,

равносильное уравнению

. (2)

Уравнение (2) является следствием исходного уравнения. Возводя обе части этого уравнения в квадрат, приходим к уравнению

, или .

Это уравнение является следствием уравнения (2) (а значит, и исходного уравнения) и имеет корни , .

Первый корень удовлетворяет исходному уравнения, а второй - не удовлетворяет.

Ответ. .

Рассмотрим пример, где реализуется проблема с "расклеиванием" корней, то есть использование формулы .

Пример 9. Решить уравнение .

Решение. Попробуем решить это уравнение разложением на множители

.

Заметим, что при этом действии оказалось потерянным решение . Посмотрите, оно подходит к исходному уравнению и уже не подходит к полученному: не имеет смысла при . Поэтому это уравнение лучше решать обычным возведением в квадрат

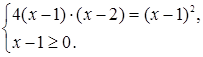
Ответ. , .

Вывод. Есть два пути. Или аккуратно возводить уравнение в квадрат, или безошибочно определять, какие решения могли быть потеряны, и проверить, не случилось ли этого на самом деле.

III. Существует еще более опасное действие - сокращение на общий множитель.

Пример 10. Решить уравнение .

"Решение". Сократим обе части уравнения на , получим

.

Нет ничего более опасного и неправильного, чем это действие. Во-первых, подходящее решение исходного уравнения было потеряно; во-вторых, было приобретено два посторонних решения . Получается, что новое уравнение не имеет ничего общего с исходным! Вот правильное решение.

Решение. Перенесем все члены в левую часть уравнения и разложим ее на множители

.

Это уравнение равносильно системе

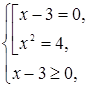
которая имеет единственное решение .

Ответ. .

Применение общих методов для решения иррациональных уравнений

1. Метод разложения на множители.

Суть этого метода заключается в следующем: уравнение можно заменить совокупностью уравнений:

; ; .

Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние. Приведем пример применения метода разложения на множители при решении иррациональных уравнений.