Методика решения иррациональных уравнений и неравенств в школьном курсе математики
неверное неравенство ![]() , мы получим верное неравенство
, мы получим верное неравенство ![]() ;
;
неверное неравенство ![]() , мы получим неверное неравенство
, мы получим неверное неравенство ![]() .
.
Вы видите, что во
зможны все комбинации верных и неверных неравенств.
Однако верно основное используемое здесь утверждение: если обе части неравенства возводят в четную степень, то получится неравенство, равносильное исходному только в том случае, если обе части исходного неравенства неотрицательны.
Поэтому основным методом решения иррациональных неравенств является сведение исходного неравенства к равносильной системе или совокупности систем рациональных неравенств.
Наиболее простые иррациональные неравенства имеют вид: ![]() (или
(или ![]() );
);
![]() (или
(или ![]() );
);
![]() (или
(или ![]() ).
).
Иррациональное неравенство ![]() (или
(или ![]() ) равносильно системе неравенств
) равносильно системе неравенств
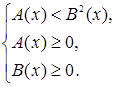 или
или 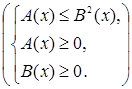 . {1}
. {1}
Первое неравенство в системе {1} является результатом возведения исходного неравенства в степень, второе неравенство представляет собой условие существования корня в исходном неравенстве, а третье неравенство системы выражает условие, при котором это неравенство можно возводить в квадрат.
Иррациональное неравенство ![]() (или
(или ![]() ) равносильно совокупности двух систем неравенств
) равносильно совокупности двух систем неравенств
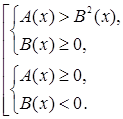 или
или 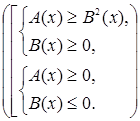 . {2}
. {2}
Обратимся к первой системе схемы {2}. Первое неравенство этой системы является результатом возведения исходного неравенства в квадрат, второе - условие, при котором это можно делать.
Вторая система схемы {2} соответствует случаю, когда правая часть отрицательна, и возводить в квадрат нельзя. Но в этом и нет необходимости: левая часть исходного неравенства - арифметический корень - неотрицательна при всех x, при которых она определена. Поэтому исходное неравенство выполняется при всех x, при которых существует левая часть. Первое неравенство второй системы и есть условие существования левой части.
Иррациональное неравенство ![]() (или
(или ![]() ) равносильно системе неравенств
) равносильно системе неравенств
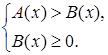 или
или 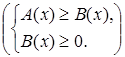 . {3}
. {3}
Поскольку обе части исходного неравенства неотрицательны при всех x, при которых они определены, поэтому его можно возвести в квадрат. Первое неравенство в системе {3} является результатом возведения исходного неравенства в степень. Второе неравенство представляет собой условие существования корня в исходном неравенстве, понятно, что неравенство ![]() выполняется при этом автоматически.
выполняется при этом автоматически.
Схемы {1}-{3} - наш основной инструмент при решении иррациональных неравенств, к ним сводится решение практически любой задачи. Разберем несколько примеров.
Пример 1. Решить неравенство ![]() .
.
Решение. Заметим, что правая часто этого неравенства отрицательна, в то время как левая часть неотрицательна при всех значениях x, при которых она определена. Поэтому неравенство решений не имеет.
Ответ. Решений нет.
Пример 2. Решить неравенство ![]() .
.
Решение. Как и в предыдущем примере, заметим, что правая часть данного неравенства отрицательна, следовательно, возводить это неравенство в квадрат нельзя. И не надо, поскольку левая часть исходного неравенства неотрицательна при всех значениях x, при которых она определена. Это означает, что левая часть больше правой части при всех значениях x, удовлетворяющих условию ![]() .
.
Ответ. ![]() .
.
Пример 3. Решить неравенство ![]() .
.
Решение. В соответствии со схемой {1} решения неравенств этого типа, запишем равносильную ему систему рациональных неравенств
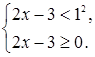
Условие ![]() выполнено при всех x, и нет необходимости добавлять его к выписанной системе.
выполнено при всех x, и нет необходимости добавлять его к выписанной системе.
Ответ. ![]() .
.
Пример 4. Решить неравенство ![]() .
.
Решение. Это неравенство решается при помощи схемы {2}. В данном случае ![]() , поэтому можно сразу записать неравенство, равносильное исходному
, поэтому можно сразу записать неравенство, равносильное исходному ![]() . Ответ.
. Ответ. ![]() .
.
Пример 5. Решить неравенство ![]() .
.
Решение. Это неравенство может быть решено при помощи схемы {1}. Система, равносильная исходному неравенству, имеет вид
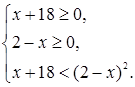
Ответ. ![]() .
.
Пример 6. Решить неравенство ![]() .
.
Решение. Данное неравенство можно решать с помощью схемы {2}. Оно равносильно совокупности двух систем
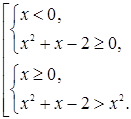
Ответ. ![]() .
.
Пример 7. Решить неравенство ![]() .
.
Решение. Согласно схеме {3}, данное неравенство равносильно системе
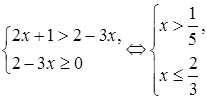
![]()
Ответ. ![]()
Более сложно решение иррациональных неравенств вида
Другие рефераты на тему «Педагогика»:
- Особенности работы над выразительностью речи глухих учащихся начальных классов
- Сравнительный анализ зарубежных и отечественных учебных пособий по физике для средней школы
- Развитие диалоговой речи у детей среднего возраста посредством театральной деятельности в детском саду
- Роль отметки в учебно-познавательной деятельности младших школьников
- Методы и формы работы социального педагога в общеобразовательном учреждении
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
