Моделирование и определение основных свойств волны Лява

Найденная скорость волны Лява носит название фазовой скорости и ее величина, помимо прочего, зависит от частоты колебаний и номера гармоники k - номера корня уравнения (17). Это означает, что в изучаемом разрезе может наблюдаться целая серия гармоник волн Лява. В реальных условиях в зависимости от параметров разреза и частоты обычно могут наблюдаться две или более гармоник (рис.1).

Из уравн

ения (17) следует, что при неограниченном увеличении частоты (ω → ∞) фазовая скорость любой гармоники волн Лява асимптотически приближается к скорости распространения поперечных волн в слое. Наоборот, при неограниченном уменьшении частоты (ω → 0) фазовые скорости всех гармоник приближаются к значению скорости распространения поперечных волн в полупространстве (рис).

Перепишем уравнение (17) в следующем виде

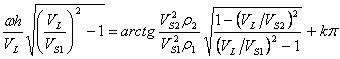, (18)

Воспользуемся тем, что

(18а)

тогда подставляя (18а) в (18), получим

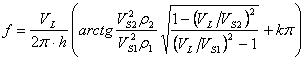. (19)

Рассмотрим предельные случаи:

Когда VL = V1 и ω → ∞, то , очевидно λ → 0.

Когда VL = V2 и ω → ∞, то λ → ∞.

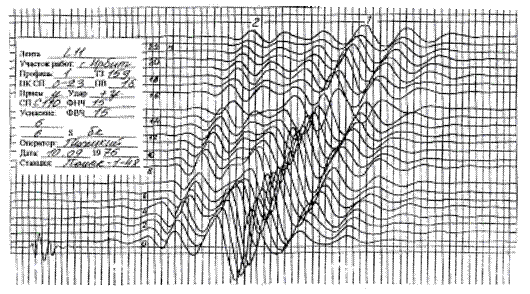
Рис.1. Запись гармоник поверхностных волн Лява: 1 - первая гармоника; 2 - вторая гармоника

Найдя корни характеристического уравнения (17) - численную зависимость фазовой скорости от частоты для конкретной гармоники k - компоненты векторов смещения в слое и полупространстве можно рассчитать по формулам:

; (18)

. (19)

Полученные формулы описывают все кинематические и динамические особенности распространения гармоник волн Лява в рассмотренной модели среды.

Расчётная часть

Теперь рассмотрим зависимость скорости волны Лява от частоты (рис.2). Здесь мы взяли следующие константы, характеризующие систему, состоящую из двух слоёв, плотностями ρ1 = 2,2 г/см3, ρ2 = 2,4 г/см3, считаем, что скорость волны в первом слое V1 = 800 м/с, а во втором - V2 = 1400 м/с. Мощность перекрывающего слоя h = 10 м. На графике изображены зависимости при различных k = 0, 1,2. Очевидно, что график 1 соответствует случаю k = 0. Заметим, что все кривые стремятся к значению VL = V1, тогда частота f стремится к бесконечности. Верхней асимптотой служит значение скорости в полупространстве. Стоит отметить, что график 1 для основной моды фазовой скорости волны Лява, а остальные - это высших гармоник.

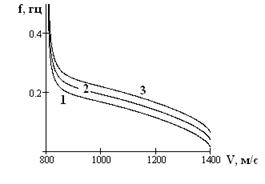
Рис.2. Зависимость частоты волны от её скорости.

Рассмотрим теперь зависимость длины волны λ от скорости волны VL. Используя формулу

Получим для тех же значений плотности, скорости и мощности h соответствующий график (рис.3).

Здесь видно, что при k = 0 мы получаем график 1, соответственно при k = 2 получим график 3. Смысл состоит в том, что при равенстве скорости волны Лява скорости в первом слое, длина волны при этом стремится к 0. И, наоборот, если скорость волны Лява приближается к скорости во втором слое, то длина волны стремится к бесконечности.

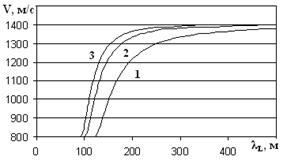
Рис.3. Зависимость длины волны от её скорости.

Тем самым, мы показали, что скорость волны целиком и полностью зависит от параметров разреза и частоты.

Список литературы

1. Бондарев В.И., 2000, Основы сейсморазведки. Екатеринбург: Изд-во УГГГА.

2. Сейсморазведка: Справочник геофизика, 1990/ Под ред.В.П. Номоконова. М.: Недра.

3. Гурвич И.И., Боганик Г.Н., 1980, Сейсморазведка. М.: Недра.

 Скачать реферат