Структурный, кинематический и силовой анализ механизма. Синтез зубчатой передачи

· м/с. (2.11)

Вектор ab изображает скорость точки В в относительном вращении вокруг точки А:

· м/с. (2.12)

Вектор О2В изображает скорость точки В в относительном вращении вокруг точки О2:

=· м/с. (2.13)

Положение точки С находим на плане скоростей по свойству подобия (из пропорции), мм:

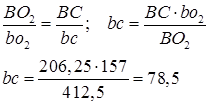(2.14)

Подставив значения длины звеньев на схеме и длины соответствующих отрезков на плане, определяем место точки С на плане скоростей. Соединив ее с полюсом, определяем значение скорости точки С, м/с:

. (2.15)

Для определения скорости точки D воспользуемся векторными равенствами:

(2.16)

где: – скорость точки С, известна по значению и направлению;

– относительная скорость точки D во вращении вокруг точки С;

Относительная скорость известна по линии действия: перпендикулярна к звену DC, проводится на плане из точки С (конец вектора ). Скорость точки D относительно стойки направлена по линии хода ползуна, проводится на плане из полюса PV параллельно ходу ползуна до пересечения с вектором относительной скорости . Точка пересечения будет точкой d. определяющей конец вектора скорости :

VD = · ; VD = 78 × 0,013 = 1,014 м/с. (2.17)

Вектор изображает скорость VDC точки D в относительном вращении вокруг точки С:

VDC = · ; VDC = 0,2 × 0,013 = 0,0026 м/с. (2.18)

Исходя из теоремы подобия (третье свойство плана скоростей), находим на плане точки S1 – S5, соответствующие центрам тяжести звеньев. Соединив их с полюсом PV, определяем скорости центров тяжести звеньев механизма, м/с:

VS = PVS1 · kV; VS = 52·0,013=0,95

VS = PVS2 · kV; VS = 70,5 × 0,013 = 2,7;

VS = VD; VS = 1,014; (2.19)

VS = PVS4 · kV; VS = 78× 0,013 =1,014

VS = PvS3·kv; VS = 78·0,013=1,014

Пользуясь планом скоростей, определяем угловые скорости звеньев 2, 3, 4, с-1:

;

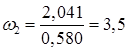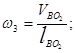
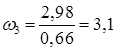; (2.20)

;

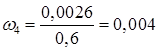Угловая скорость ползуна w5 = 0, так как он движется поступательно по неподвижной направляющей.

Для выяснения направления угловой скорости звена АВ вектор скорости , направленной к точке b плана, мысленно переносим в точку В звена 2 и определяем, что он стремится повернуть это звено вокруг точки А против часовой стрелке. По аналогии определяем направления угловых скоростей звеньев w4 (против часовой стрелки) и w3 (против часовой стрелки).

2.6 Определение ускорений точек механизма методом планов ускорений

При помощи планов ускорений можно найти ускорения любых точек механизма. Для построения планов ускорений по аналогии с планами скоростей следует пользоваться их свойствами. Свойства такие же, как и у планов скоростей, кроме третьего, где фигура, подобная одноименной жесткой фигуре на плане положений механизма, повернута на угол (180° – j¢) в сторону мгновенного ускорения e данного звена,

где . (2.21)

Поскольку полные относительные ускорения состоят из геометрической суммы тангенциальных и нормальных составляющих, то концы векторов абсолютных ускорений обозначают буквами, соответствующими названию точек.

Считая известными ускорения шарнирных точек (аО = аО = 0), помещаем их на плане ускорений в полюсе рa. Звено О1А вращается равномерно, поэтому точка А имеет только нормальное ускорение , которое направлено по звену О1А к центру вращения О1 (см. рис. 2.3, в). Определяем его по формуле, м/с2 :

; . (2.22)

Принимаем (произвольно) длину отрезка , изображающего вектор ускорения точки А, равной 180 мм. Тогда масштаб плана ускорений, м/с2×мм-1,

; . (2.23)

 Скачать реферат