Использование линейного программирования для решения задач оптимизации

Рефераты / Экономико-математическое моделирование / Использование линейного программирования для решения задач оптимизации

Система ограничений канонической формы задачи линейного программирования может быть соответственно переписана в виде:

$\begin{displaymath}Ax = A_Bx^B + A_Nx^B = b.\end{displaymath}$ (3)

Предположим, что матрица $A_B$ имеет полны

й ранг, т.е. $A_B$ - невырожденная. Тогда из равенства (5) следует

$\begin{displaymath}x^B = (A_B)^{-1}b.\end{displaymath}$ 4)

Целевая функция задачи ЛПР также может быть разбита на базисную и не базисную части:

$\begin{displaymath}cx = c_Bx^B + c_Nx^N.\end{displaymath}$

Подстановка (6) дает

$\begin{displaymath}cx = (c_N + c_B(A_B)^{-1}A_N) = d^Nx^N.\end{displaymath}$ 5)

Предположим, что мы находимся в некоторой начальной точке $x^0 = (x^B_0,0)$ со значением целевой функции

$\begin{displaymath}cx^0 = c_B(A_B)^{-1}b.\end{displaymath}$

Каким образом можно уменьшить далее значение целевой функции? Из соотношения (5) следует, что для этого достаточно сделать положительными те компоненты вектора $x^N$ , которым соответствуют отрицательные значения координат вектора модифицированных стоимостей

$\begin{displaymath}d^N =c_N + c_B(A_B)^{-1}A^N, \end{displaymath}$

сохраняя при этом неотрицательность базисных переменных $x^B$ .

Увеличение $x^N$ может быть проделано различным образом, и за время существования симплекс-метода были проделаны многочисленные эксперименты по поиску наиболее эффективных стратегий увеличения $x^N.$

Здесь будет рассмотрена простейшая:

· среди компонент вектора $d^N = (_i, i \in N)$ находится минимальная;

· соответствующая небазисная переменная $x^N_i$ получает максимально возможное приращение, сохраняющее неотрицательность базисных переменных.

Поскольку при увеличении $i$ -й компоненты вектор $x^N$ приобретает вид:

$\begin{displaymath}x^N = \lambda e^i, \end{displaymath}$

где $e^i$ это $i$ -й орт, а $\lambda$ -- степень увеличения этой переменной или шаг алгоритма, то модифицированный базисный вектор выражается следующим образом:

$\begin{displaymath}x^B = (A_B)^{-1}b - \lambda(A_B)_{-1}A^Ne^i \equiv \beta - \lambda \alpha,\end{displaymath}$

где $\alpha$ - $i$ -й столбец матрицы $(A_B){-1}A^N.$ Шаг $\lambda$ определяется при этом из условия:

$\begin{displaymath}\beta - \lambda \alpha \geq 0.\end{displaymath}$

Максимально возможное значение $\lambda$ определится при этом как

$\begin{displaymath}\lambda = \min_{\alpha_i > 0} \frac{\beta_i}{\alpha_i}.\end{displaymath}$ 6)

Пусть $k$ -- номер $i$ , на которой достигается минимум (6). Очевидно, что при этом

$\begin{displaymath}x^B_k = \beta_k - \lambda \alpha_k = 0.\end{displaymath}$

При этом говорят, что переменная $x^B_k$ выводится из базиса (обращается в нуль), а переменная $x^N_i$ вводится в базис. Целевая функция при этом уменьшается на величину

$\begin{displaymath}\delta cx = \lambda d^N_i.\end{displaymath}$

Важную роль в теории симплекс-метода играет условие невырожденности, в котором предполагается полный ранг AB и строгая положительность базисного решения β. При этом λ > 0 и δcx < 0, то есть целевая функция уменьшается при переходе к новому базису.

Поскольку в задаче линейного программрования может быть лишь конечное число базисов, а на каждой итерации происходит уменьшение целевой функции, базисы не могут повторяться. Следовательно, после конечного числа итераций вектор модифицированных стоимостей станет неотрицательным, а это означает, что дальнейшее уменьшение целевой функции невозможно, т.е. будет получено одно из оптимальных решений.

В силу выпуклости задачи любое другое оптимальное решение будет иметь также значение целевой функции, т.е. будет в этом смысле эквивалентно.

Геометрический метод

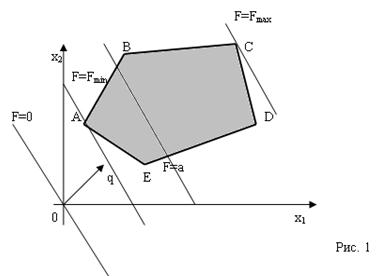
Рассмотрим задачу линейного программирования в стандартной форме с двумя переменными (n = 2). К такой форме может быть сведена и каноническая задача (с ограничениями в виде уравнений), когда число переменных n больше числа уравнений m на 2, т. е. n – m = 2.

Пусть геометрическим изображением системы ограничений является многоугольник ABCDE (рис. 1). Необходимо среди точек этого многоугольника найти такую точку, в которой линейная функция F=c1x1+c2x2 принимает максимальное (или минимальное) значение.

Скачать реферат

Страница: 1 2 3 4 5 6

Использование линейного программирования для решения задач оптимизации

Другие рефераты на тему «Экономико-математическое моделирование»:

Поиск рефератов

Последние рефераты раздела