Методы линейного программирования для решения транспортной задачи

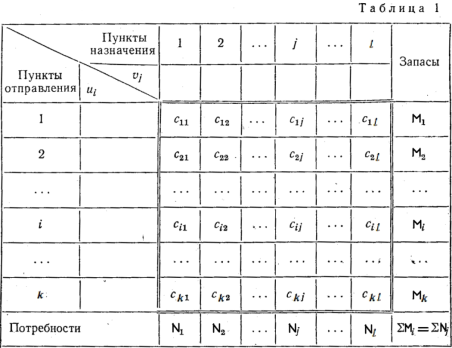
Основная часть макета выделена двойными линиями. Она содержит k×l клеток. Каждая клетка в этой части обозначается символом (i, j). Например, клетка, стоящая во второй строке и первом столбце, будет обозначена (2, 1). Макет содержит в себе матрицу тарифов. Назначение строки vj и столбца ui будет выяснено в дал

ьнейшем.

Прежде чем приступить к изложению метода, рассмотрим некоторые предварительные понятия.

Произвольную совокупность клеток в макете называют набором. Цепью называется последовательный набор клеток, в котором каждые две соседние клетки расположены в одном ряду (строке, столбце), причем никакие три клетки в одном ряду не располагаются.

Пример цепи приведен в табл.2.

Прямые, соединяющие взятые клетки, пересеклись, но так как клетку в пересечении мы не берем, правило цепи не нарушается.

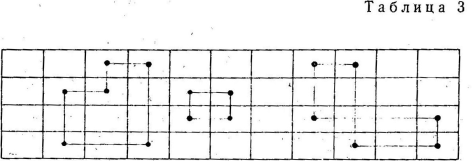
Если последняя клетка цепи расположена в одном ряду с первой, то такая замкнутая цепь называется циклом. Некоторые разновидности циклов показаны в табл.3.

Теорема. Пусть в макете (или матрице) из k строк и l столбцов произвольно отмечено k+l клеток, причем k+l £ kl. В этом случае всегда можно построить цикл, вершины которого лежат в отмеченных клетках (может быть не во всех).

Замечание. Числа k и l целые, и для них не всегда будет выполнено неравенство k+l £ kl. Если одно из этих чисел - единица, это неравенство не выполняется. Например, при k=3, l=1 имеем 3 + 1 > 3·1. Однако при k=2 и l=2 будет 2+2 = 2·2, а при k и l, одновременно больших двух, неравенство всегда выполняется.

Условие k+l £ kl исключает случаи матриц с одной строкой или одним столбцом, в которых вообще цикла построить нельзя.

Доказательство. Рассмотрим минимальный возможный случай: k=2, l=2 (табл.4).

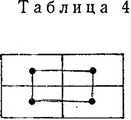
В макете надо выбрать k+l = 4, т.е. все 4 клетки. Для этого случая теорема справедлива: выбранные клетки образуют цикл.

Возьмем теперь любые k>2, l>2. Доказательство будем вести методом математической индукции.

Допустим, теорема справедлива для макета, у которого сумма строк и столбцов на единицу меньше взятых нами (k+l). Докажем, что при этом предположении теорема будет справедлива для принятых (k+l).

Первый случай. Среди отмеченных клеток имеется одна клетка, единственная в ряду (строке или столбце) (табл.5).

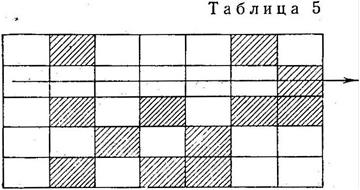
Откажемся от этой клетки, исключим эту строку из рассмотрения. Тогда придем к таблице, у которой строк на единицу меньше, а число столбцов сохранилось. Число строк в сумме с числом столбцов будет меньше (k+l) на одну единицу, но и число отмеченных клеток уменьшится на одну. Для этого случая можно построить цикл по принятому допущению. Этот цикл возьмем и для нашей таблицы, так как в соответствии с оговоркой вершины цикла могут быть и не вo всex отмеченных клетках.

Второй случай. Нет таких ситуаций, когда клетка одна. В каждой строке (столбце) больше чем одна клетка (или нет ни одной) (табл.6).

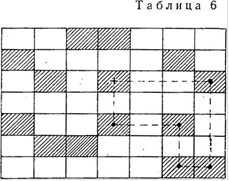
Отметим одну клетку знаком плюс, пойдем от нее по строке, попадем в клетку, которая в другом столбце и неединственная в нем; по столбцу перейдем в другую строку, по этой строке в другой столбец и т.д. Это можно было бы продолжать до бесконечности, если бы не было конечным число отмеченных клеток. На каком-то этапе придем в строку (столбец), в которой уже были, чем будет замкнута цепь, т.е. получен цикл.

Выше было показано, что теорема справедлива для k=2, l=2, т.е. для k+l=4. По доказанному она справедлива для случаев: k+l=5, т.е. k+l>4; k+l=6, т.е. k+l>5; k+l>6 и т.д., т.е. для любого макета.

Допустимый план Х (xij) называется ациклическим (нециклическим), если набор клеток с отличными от нуля компонентами плана xij>0 не содержит ни одного цикла.

Пример ациклического плана приведен в табл.7,

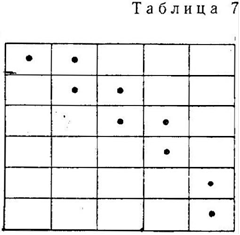
где точки обозначают клетки, в которых xij >0 (xij<0 недопустимы по смыслу задачи). Как покажем ниже, среди ациклических планов есть оптимальный.

Если в ациклическом плане Х (xij) число положительных компонентов

N = k + l - 1 (остальные компоненты - нули), то элементы aij матрицы тарифов из набора клеток, в которых расположены xij >0, будем называть Х-отмеченными.

Если же число положительных компонент плана N < k + l - l, то к клеткам, занятым положительными xij добавляем недостающие до (k+l-1) из нулевых клеток, лишь бы присоединенные клетки вместе с уже взятыми не допускали циклов. Тарифы aij всех взятых клеток, равно как и сами клетки, включаются в число Х-отмеченных.

Больше (k + l - 1) число компонент ациклического плана не может быть: , так как уже при N=k+l по доказанной выше теореме всегда из выбранных клеток можно построить цикл.

Теорема 2 (основная теорема). Если для некоторого плана Х= (xij) kl транспортной задачи можно подобрать систему из k+l чисел u1, u2,…, ui,…, uk; vl, v2,…, vj,…, vl, удовлетворяющую следующим условиям: vj - ui £ aij для всех i = 1, 2,., k; j = 1, 2,., l, а для xij>0 (xij (-X)) vj - ui = aij, то план Х будет оптимальным.

Числа ui, vj называются потенциалами пунктов отправления и пунктов назначения; условия vj - ui £ aij и vj - ui = aij называют условиями потенциальности плана Х.

К каждой клетке (i, j) относятся два потенциала: i-ro пункта отправления ui и j-ro пункта назначения vj. Условия потенциальности словесно можно сформулировать так: разность потенциалов для всех без исключения клеток должна быть меньше или равна тарифу, а для занятых (Х-отмеченных) клеток она должна быть точно равна тарифу. План, удовлетворяющий этим условиям, называется потенциальным.

С учетом такой терминологии основную теорему можно изложить короче: если некоторый план транспортной задачи потенциален, то он оптимален.

Доказательство. Допустим, что для некоторого плана Х (xij) условия потенциальности выполнены, т.е. существует такая система чисел ui и vj, которая удовлетворяет условиям vj - ui = aij и vj - ui £ aij (табл.8).

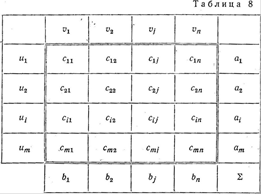
Иными словами, пусть план Х потенциален. Докажем, что этот план будет оптимальным. План Х дает значение функционалу

.

Так как мы еще не знаем, оптимален план Х или нет, то возьмем заведомо оптимальный план Х' (x¢ij) и посмотрим, какое значение он доставляет функционалу:

 Скачать реферат