Определение реакции опор твёрдого тела

«Определение реакции опор твёрдого тела»

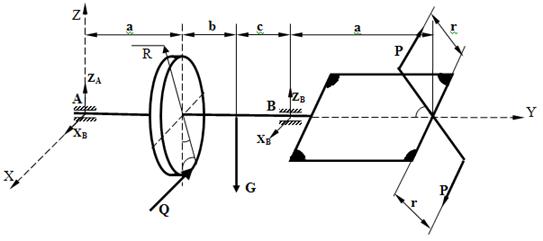
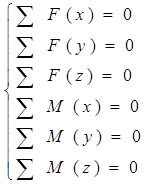
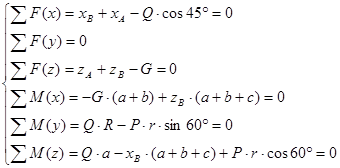
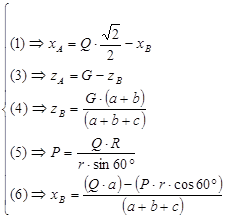
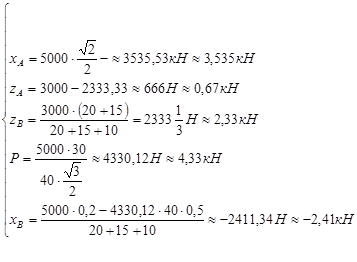
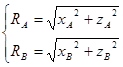
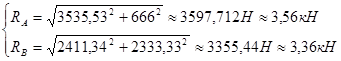
Результаты вычислений приведены в таблице:

При нахождении получилось, что значение составляющей по оси отрицательно. Это значит, что при расставлении действующих на данную систему сил было выбрано неверное направление. В итоге правильное построение будет выглядеть следующим образом:

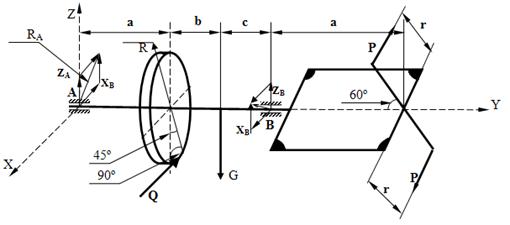
«Определение скорости и ускорения точки по заданным уравнениям её траектории».

1. Скорость

В общем случае для пространственной системы координат будем иметь:

=>

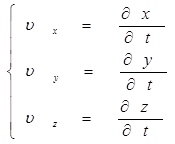Для нашего случая уравнения для составляющих по осям координат будут иметь следующий вид:

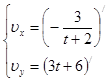
После дифференцирования получим:

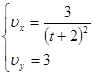
Найдём полную скорость точки в момент времени :

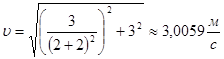
2. Ускорение

В общем случае для пространственной системы координат будем иметь:

=>

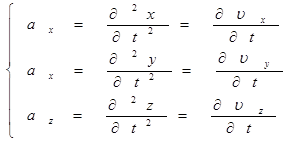Для нашего случая уравнения для составляющих по осям координат будут иметь следующий вид:

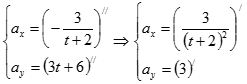
После дифференцирования получим:

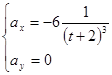
Найдём полное ускорение точки в момент времени :

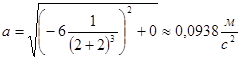
С другой стороны ускорение можно найти по формуле:

, где

тангенциальное ускорение (касательная составляющая полного ускорения), а нормальная составляющая полного ускорения, которые можно найти по формулам:

,

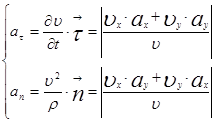где - радиус кривизны траектории в искомой точке.

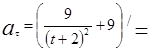-0,0058 при =2 с.

Тогда найдётся по формуле:

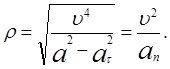
Подставив значения, получим:

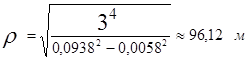
Найдём уравнение движения точки. Для этого выразим из второго уравнения переменную времени () и подставим полученное выражение в первое уравнение:

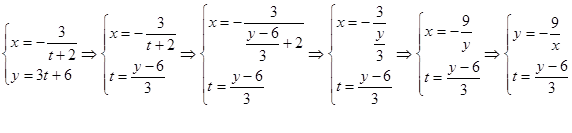
Получившееся уравнение () является гиперболой.

 Скачать реферат