Рассеяние рентгеновских лучей на молекулах фуллерена

Как известно, ускорение частицы (по основному закону динамики) прямо пропорционально силе, действующей на частицу. Следовательно, если сила прямо пропорциональна координате с обратным знаком, то частица будет совершать гармоническое колебание. Такие силы называются возвращающими.

Важным примером возвращающей силы является сила Гука (упругая сила). Таким образом, если на материальную точку д

ействует сила Гука, то точка совершает гармонические колебания.

Так как мы рассматриваем одномерные колебания, то для анализа задачи достаточно спроецировать вектор силы Гука на ось, параллельную этой силе. Если ноль отсчета координаты x выбран в точке, в которой возвращающая сила равна нулю, то проекция силы равна

Fx = - k x,(1.8)

где коэффициент k называется жесткостью.

Сравнивая уравнения (1.7) и (1.8), и используя 2-й закон Ньютона, получим важное выражение для частоты колебаний:

w2 = k / m(1.9)

Это означает, что частота колебаний описывается параметрами физической системы, а не зависит от начальных условий. В частности, выражение (1.9) определяет частоту гармонических колебаний систем, показанных на рис.1.1. и 1.2.

В качестве поучительно примера рассмотрим одномерные движения, которые совершают грузы, прикрепленные к пружинам (см. рис.1.8).

Рис.1.8. Грузы на пружинах.

Пусть массы пружин пренебрежимо малы по сравнению с массами грузов.

Грузы рассматриваются как материальные точки.

Сначала рассмотрим систему, изображенную на рис.18. а. Предположим, что первоначально груз был смещен влево и, как следствие пружина растянулась. При этом на груз (материальную точку) действуют 3 силы: сила тяжести mg, сила упругости F и сила нормальной реакции опоры N. Трением в данной задаче мы пренебрегаем (см. рис.1.9).

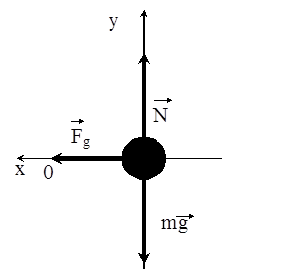
Рис.1.9. Силы на груз, лежащий на гладкой опоре, при растяжении пружины.

Запишем второй закон Ньютона для тела, изображенного на рис.1.9.

ma = mg + F + N(1.10)

Сила упругости при небольших деформациях пружин описывается законом Гука

F = – k d(1.11)

где d – вектор деформации пружины, k – коэффициент жёсткости пружины.

Заметим, что при движении груза растяжение пружины может сменяться сжатием. При этом вектор деформации d будет менять свое направление на противоположное, следовательно, то же будет происходить с силой Гука (1.11). Из этого, в частности, следует, что при начальном сжатии пружины векторное уравнение движение (1.10) будет иметь тот же вид:

ma = mg – k d + N(1.12)

Выберем начало координат в точке расположения груза при недеформированной пружине. Ось X направим горизонтально, ось Y –вертикально, т.е. перпендикулярно опоре (см. рис.1.9).

Так как груз движется вдоль опоры по горизонтали, то проекция ускорения на ось Y равна нулю. Тогда сила тяжести полностью компенсируется нормальной реакции опоры

N + mg = 0 (1.13)

Проецирование уравнения движения (1.12) на ось X дает скалярное уравнение:

ma = – kd,(1.14)

где a – горизонтальная проекция ускорения груза, d – проекция вектора деформации пружины.

Иначе говоря, ускорение направлено по горизонтальной оси X и равно

a = – (k/m) d(1.15)

Еще раз заметим, что уравнение (1.15) справедливо и при растяжении, и при сжатии пружины.

Так как начало координат выбрано так, что оно совпадает с концом недеформированной пружины, то проекция деформации совпадает со значением горизонтальной координаты груза x:

a = – (k/m) x (1.16)

По определению проекция ускорения равна второй производной соответствующей координаты по времени. Следовательно, одномерное уравнение движения (1.16) можно переписать в виде

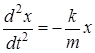(1.17)

Иначе говоря, проекция ускорения прямо пропорциональна координате, причем коэффициент пропорциональности имеет отрицательный знак.

Уравнение (1.17) является дифференциальным второго порядка, общая теория решения таких уравнений изучается в курсе математического анализа. Однако легко доказать непосредственной подстановкой, что функция гармонических колебаний (1.3) удовлетворяет уравнению (1.17). Как уже было доказано ранее, частота колебаний выражается формулой (1.9).

Амплитуда A и начальная фаза j0 колебаний определяются из начальных условий.

Пусть первоначально груз был смещен вправо от положения равновесия на расстояние d0, а начальная скорость груза равна нулю. Тогда используя функции (1.3) и (1.5), запишем для момента времени t=0 следующие уравнения:

d0 =A cos(j0) (1.18)

0 = - w A sin(j0) (1. 19)

Решением системы (1.18) – (1. 19) являются следующие значения A = d0 и j0= 0.

Для других начальных условий величины A и j0, естественно приобретут другие значения.

Теперь рассмотрим систему, изображенную на рис.1.8. б. На груз в этом случае действуют только две силы: сила тяжести mg и сила упругости F (см. рис.1.10). Ясно, что в положении равновесия эти силы компенсируют друг друга, следовательно, пружина растянута.

Пусть груз несколько смещается по вертикали. Тогда векторное уравнение движение будет иметь вид, аналогичный уравнению (1.12)

ma = mg – k d(1. 20)

причем независимо от направления вертикального смещения (вверх или вниз).

Все векторы в уравнении (1. 20) направлены вертикально, поэтому это уравнение целесообразно спроецировать на вертикальную ось координат. Направим ось вниз, а начало координат выберем в точке, где тело находится в состоянии равновесия (см. рис.1.10).

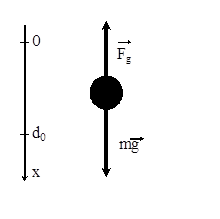
Рис.1.10. Силы, действующие груз, висящий на пружине.

Спроецировав (1.18) на ось X получим:

a = g – (k/m) d(1.21)

где a – проекция ускорения тела, d – проекция деформации пружины.

Для решения уравнения (1.21) полезно вернуться к положению равновесия груза. Уравнение Ньютона для этого положения имеет вид:

0 = g – (k/m) d0(1.22)

где d0 –деформации пружины при равновесии груза. Следовательно, вектор d0 равен

d0 = mg/k(1.23)

Видно, что в положении равновесия тела пружина действительно растянута, так как вектор d0 направлен параллельно вектору g, т.е. вниз.

Теперь поместим начало координат в точке равновесия груза на пружине, и тогда уравнение (1.21) примет вид:

a = g – (k/m) (x+ d0) (1.24)

где d0 –модуль вектора деформации пружины d0.

Подставив в уравнение (1.24) величину d0, полученную из соотношения (1.23), получим:

a = g – (k/m) (x+ (m/k) g)

или

a = – (k/m) x (1.25)

Полученное уравнение полностью совпадает с уравнением (1.16). Таким образом, тело, изображенное на рис.1.8. б, совершает также гармоническое колебательное движение, описываемое функцией (1.3), как и груз в системе, изображенной на рис.1.8. а. Частота колебаний Отличие заключается лишь в направлении колебаний (вертикальное вместо горизонтального). Но частота колебаний по-прежнему определяется жесткостью пружины и массой груза формулой (1.9).

 Скачать реферат