Гармонические колебания в параллельном контуре
1. Основные параметры колебательного контура
Пусть конденсатор С, заряженный от внешнего источника, подключается к индуктивности L (рис. 1а)
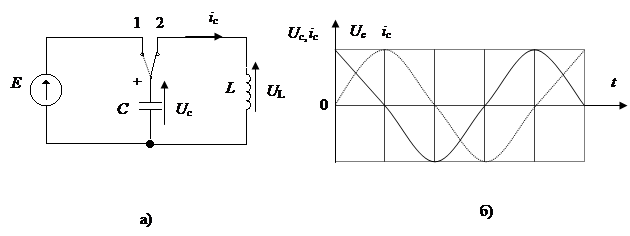 |
Разряд конденсатора не мо
жет произойти мгновенно, т.к. этому препятствует ЭДС самоиндукции, возникающая в элементе индуктивности.
В идеальном контуре, активное сопротивление которого равно нулю, и, следовательно, отсутствуют потери, запасенная в электрическом поле энергия полностью переходит в энергию магнитного поля индуктивности.
Затем происходит обратный переход энергии. Далее процессы повторяются. Таким образом, возникают незатухающие электрические колебания, имеющие форму косинусоиды. Графики ![]() и
и ![]() представлены на рисунке 1, б.
представлены на рисунке 1, б.
Частота, с которой происходит колебания энергии между реактивными элементами при отключении источника, называется частотой свободных (собственных) незатухающих колебаний контура. Обозначение: ![]() или
или ![]() .
.
Т.к. в идеальном контуре величины напряжений на L и C одинаковы, то
![]() ,
, 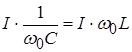 ,
,
![]() или
или ![]() ,
, ![]() .
.
В режиме свободных колебаний через элементы контура протекает ток. Сопротивление, которое оказывают элементы контура току на частоте собственных колебаний, называется волновым (характеристическим).
Это сопротивление обозначается ![]() и определяется следующим образом:
и определяется следующим образом:
![]() , или
, или 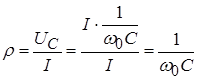 . Т.к.
. Т.к. ![]() , то
, то
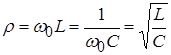 (Ом).
(Ом).
Из последнего выражения следует, что на частоте собственных колебаний![]() волновое сопротивление равно одному из реактивных сопротивлений (рис. 2).
волновое сопротивление равно одному из реактивных сопротивлений (рис. 2).
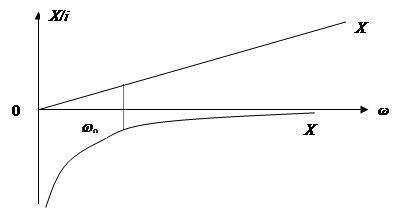
Рис. 2
На практике реальный КК всегда имеет потери активное сопротивление не равно 0, что приводит к затухающему характеру свободных колебаний (рис. 3).
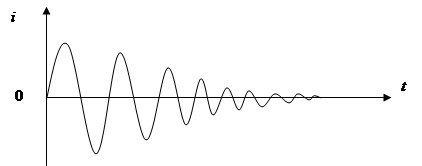 Рис. 3
Рис. 3
Для характеристики последнего свойства вводится понятие добротность контура (качество контура).
Добротность ![]() является энергетическим параметром и показывает во сколько раз реактивная мощность (за счет которой и происходят свободные колебания) больше активной:
является энергетическим параметром и показывает во сколько раз реактивная мощность (за счет которой и происходят свободные колебания) больше активной:
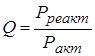
Отметим, что данное определение относится не только к колебательным контурам, но и к отдельным деталям, например, к катушкам индуктивности, к конденсаторам.
Чем больше реактивная мощность, тем выше добротность и тем медленнее происходит затухание колебаний и наоборот.
Добротность КК, применяемых в технике связи, обычно составляет десятки-сотни, а в технике СВЧ и специальных устройствах добротность может достигать тысячи и больше.
Принято считать, что если: ![]() – KK низкой добротности,
– KK низкой добротности,
![]() – КК средней добротности,
– КК средней добротности,
![]() – КК высокой добротности.
– КК высокой добротности.
Практически реализовать LC контур с добротностью свыше 400 трудно из-за низкой добротности катушек индуктивности (именно они и определяют качество контура).
Вывод: Рассмотренные параметры ![]() ,
, ![]() и
и ![]() для колебательных контуров являются одним из основных, т.к. они зависят от первичных параметров, и их называют вторичными параметрами контура.
для колебательных контуров являются одним из основных, т.к. они зависят от первичных параметров, и их называют вторичными параметрами контура.
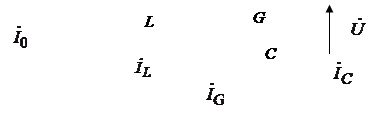
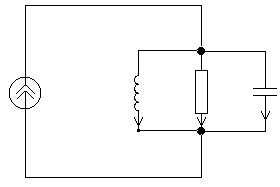
Рис. 4
2. Возможные режимы установившихся гармонических колебаний в параллельном колебательном контуре
Параллельным колебательным контуром называют цепь, составленную из элементов индуктивности, емкости и сопротивления, соединенных параллельно. Схема контура показана на рисунке 4.
Найдем комплексную проводимость контура:
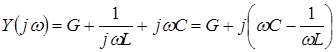 ,
,
где: ![]() – активная составляющая проводимости,
– активная составляющая проводимости,
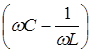 – реактивная составляющая проводимости.
– реактивная составляющая проводимости.
Из формулы следует, что в зависимости от соотношения ![]() и
и ![]() в параллельном контуре возможны 3 режима:
в параллельном контуре возможны 3 режима:
1) ![]() , т.е.
, т.е. ![]() и
и ![]() .
.
Построим для этого случая векторную диаграмму, положив начальную фазу напряжения на контуре, равной 0 (рис. 5)
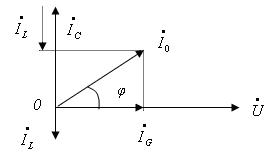
Рис. 5
Как видно из векторной диаграммы, ток в контуре опережает напряжение на некоторый угол ![]() , что является признаком емкостного режима.
, что является признаком емкостного режима.
Вывод: При ![]() в параллельном контуре устанавливается емкостной режим колебаний и ток в контуре опережает напряжение.
в параллельном контуре устанавливается емкостной режим колебаний и ток в контуре опережает напряжение.
2) ![]() т.е.
т.е. ![]() и
и ![]() .
.
Построив аналогичным образом векторную диаграмму (рис. 6), убедимся в том, что ток в контуре будет теперь отставать от напряжения ![]() на некоторый угол
на некоторый угол ![]() , что является признаком индуктивного режима.
, что является признаком индуктивного режима.
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода
