Уравнение Шрёдингера для простейших стационарных движений

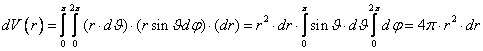.(6.13)

6.6.2. Лапласиан. Очень важным свойством лапласиана является его симметрия ко взаимным перестановкам декартовых координат.

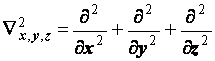(6.14)

Простейшее дифференциальное уравнение, в котором лапласиан играет основную роль - уравнение Лапласа. Это дифференциал

ьное уравнение в частных производных второго порядка. В различные квантово-механические задачи о сферических системах лапласиан входит в качестве основного оператора. Симметрия конкретной системы предопределяет вид координат, к которым следует преобразовать лапласиан, а далее и вид решений тех дифференциальных уравнений, у которых уравнение Лапласа можно выделить в качестве однородной части. Таковы задачи о сферически симметричных движениях. В шаровых координатах лапласиан оказывается составленным из трёх независимых компонент-операторов, каждый из которых преобразует лишь одну из трёх независимых пространственных переменных.

6.6.3. Перевод лапласиана в шаровые координаты можно осуществить, используя различные схемы. В сферических координатах он выглядит довольно внушительно, но при ближайшем рассмотрении оказывается достаточно простой конструкцией. Несложные, но длительные, преобразования приводят к следующей формуле:

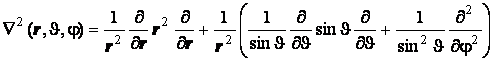. (6.15)

Упрощая, выделим вначале операторы чисто радиальный и чисто угловой:

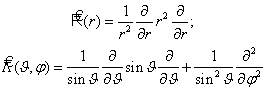.(6.16)

6.6.4. Операторные компоненты лапласиана. Первое слагаемое активно только к радиальной переменной, второе же - к угловым аргументам и оно называется оператором Лежандра. Лапласиан получает вид

. (6.17)

6.6.5 Угловой оператор - оператор Лежандра далее также разделяется на два независимых оператора. Один из них действует на переменную широты J, а второй - на переменную долготы j, так что получается:

. (6.18)

6.7. Сферическим уравнением Лапласа назовём дифференциальное уравнение в частных производных второго порядка

.(6.19)

В сферических переменных оно приобретает вид

, (6.20)

Решения отыщем по методу Фурье. Для разделения переменных искомое решение представим как произведение радиальной и угловой функций.

Общее правило: Если в дифференциальном уравнении в частных производных можно выделить оператор, включающий несколько переменных, и привести его к аддитивной форме, придавая ему вид суммы слагаемых, определённых лишь для отдельных переменных, то исходное дифференциальное уравнение распадается на систему дифференциальных уравнений. Каждое из них и их решения определены лишь на переменных соответствующего оператора-слагаемого. Частные решения исходного дифференциального уравнения выбираются в мультипликативном виде, как произведения функций – решений отдельных уравнений системы. Этот результат сформулируем в виде краткого правила: «Оператор аддитивен-Решения мультипликативны». Этот подход встречается всюду в теории многоэлектронных систем – атомов и молекул.

6.7.1. Радиальную часть общего решения сферического уравнения Лапласа выбирают в простейшем виде степенной функции от радиальной переменной, Показатель степени l полагают целочисленным неотрицательным числом . Только в этом случае соблюдается симметрия общего решения по отношению ко взаимным перестановкам декартовых координат, и делается возможно построение регулярных решений (функций класса Q ), (конечных, однозначных и непрерывных), (далее нормированных).

. (6.21)

Угловые сомножители общего решения Y(J,j) называются сферическими гармониками (шаровыми функциями). Запишем уравнение Лапласа, и рассмотрим процедуру разделения переменных:

. (6.22)

Подставим радиальный оператор и совершим следующие простейшие преобразования:

.

Перенесём одно из слагаемых в сторону от знака равенства и разделим обе части на Y(J,j):

.

6.7.2. Итоговое дифференциальное уравнение называется уравнением Лежандра.

Оно включает лишь угловую часть лапласиана и имеет вид:

. (6.23)

Уравнение Лежандра, встречается в нескольких фундаментальных задачах: 1) в задаче о квантовых состояниях и энергетических уровнях ротатора - линейной молекулы, свободно вращающейся вокруг центра массы. 2) в уравнении Шрёдингера для атома H и водородоподобных ионов.

6.7.3. Уравнение Лежандра это вполне типичное операторное уравнение на собственные функции и собственные значения. С точностью до постоянного множителя уравнение Лежандра идентично операторному уравнению на собственные значения для оператора квадрата момента импульса. Напомним вид самого оператора момента импульса:

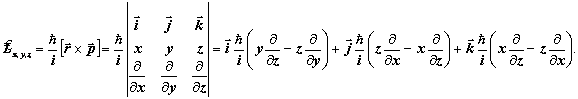
Перенесём постоянный множитель влево, получим

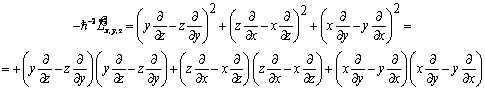(6.24)

6.7.4. Преобразуя оператор слева от знака равенства к шаровым переменным, получаем не что иное, как оператор Лежандра, т.е.:

. (6.25)

На этом основании решения уравнения Лежандра являются решениями также и операторного уравнения на собственные значения квадрата момента импульса. Отсюда строго получается формула для квантования модуля и проекции момента импульса. Это означает

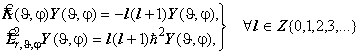. (6.26)

6.7.5. Квадрат модуля момента импульса определяется собственными значениями оператора Лежандра. Допустимые значения модуля момента импульса свободно вращающейся вокруг центра масс квантовой системы (жесткого ротатора) следуют из операторного уравнения (6.25):

. (6.27)

Соответственно при пространственном вращении возможные дискретные значения модуля момента импульса и его проекций на ось вращения определяется двумя формулами

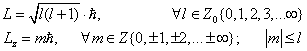(6.28)

6.8. Ротатор. Вращательные состояния ротатора . Углы прецессии момента импульса. Энергетические уровни ротатора непосредственно связаны с квадратом момента.

.(6.29)

 Скачать реферат