Разработка методики введения определения "асимптота"

Асимптота (вертикальная, горизонтальная, наклонная) - разработать методику введения определения «асимптота»

1. Мотивация

Построить и исследовать графики следующих функций:

а) y=

б) y=

в) y=x+

а) y=

(Если учащиеся не помнят график данной функции- гиперболы, строим его по точкам)

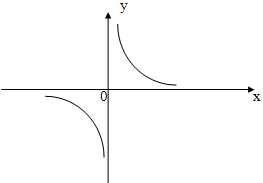
Найдем область определения и значений данной функции.

Какой промежуток является областью определения данной функции? Любое значение может принимать x?

х принимает любое значение, кроме 0, так как на ноль делить нельзя.

D(f)=(-;0);+)

Область значений:

E(f)= (-;0);+)

Является ли данная функция четной, нечетной, периодической?

f(x)=

f(-x)=1/(-x)=-; -f(x)=-

f(x)f(-x)

f(-x)=-f(x)

Функция является нечетной, график симметричен относительно начала координат, не периодическая.

Есть точки пересечения с осями координат?

Таких точек нет.

Является ли данная функция возрастающей, или убывающей?

Функция убывающая, х=0 является точкой разрыва.

Имеет данная функция точки максимума, минимума?

Нет.

Как себя ведёт данная функция в окрестности точек не входящих в область определения данной функции? В нашем случае, в окрестности точки х=0.

Как себя ведет функция?

График приближается к оси Oy. Но никогда её не пересечёт.

А пересекается ли гипербола с осью Ox?

График приближается к оси Ox, не пересекает её.

б) y=

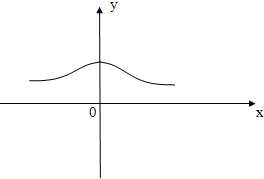
Найдем область определения и значений данной функции.

Какой промежуток является областью определения данной функции? Любое значение может принимать x?

х принимает любое значение

D(f)=(-;+)

Область значений: E(f)=;+)

Является ли данная функция четной, нечетной, периодической?

f(x)=

f(-x)==; -f(x)=-

f(-x)- f(x)

f(x)=f(-x)

Функция является четной, график симметричен относительно оси ординат, не периодическая.

Есть точки пересечения с осями координат?

Есть точки пересечения с осью Oy, x=0 y=1

Является ли данная функция возрастающей, или убывающей?

Функция возрастает на промежутке (-;0),

убывает на промежутке ;+)

Имеет данная функция точки максимума, минимума?

Точка максимума x=0 y=1

Как себя ведёт график данной функции приближаясь к оси Ох, пересечет ли он эту ось?

График приближается к оси Ox, не пересекает её.

в) y=x+