Статистическая механика классических систем

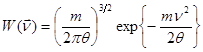(8.24)

Выражение (8.24) представляет распределение Максвелла по скоростям частиц.

С математической точки зрения распределение (8.23) и, соответственно (8.21), представляет распределение Гаусса около среднего значения с дисперсией

src="images/referats/9147/image074.png"> (8.25)

Выражение (8.25) было получено без привлечения каких-либо дополнительных соображений, поэтому позволяет установить связь между температурой со средней кинематической энергией частиц. Из (8.25) непосредственно следует:

Тогда:

,

Отсюда

, (8.26)

В некоторых работах соотношение (8.26) обосновывается с помощью дополнительных соображений и позволяет интерпретировать температуру как меру средней кинетической энергии . Однако соотношение (8.26), во-первых, получено только для классических систем. Во-вторых, интерпретация температуры как мера средней кинетической энергии частиц требует привлечения других механизмов ( не связанных с понятием температуры) для определения этой энергии.

Поэтому соотношение (8.26) следует рассматривать как интегральный, но все-таки частный результат.

Далее рассмотрим идеальный газ, находящийся во внешнем потенциальном поле. Гамильтониан такой системы оказывается равным:

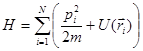(8.27)

Подставляя (8.27) в (8.10) с точностью до постоянного сомножителя имеем:

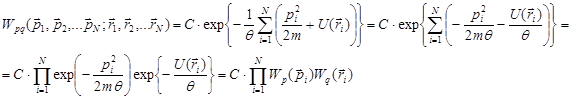(8.28)

Таким образом, гиббсовское распределение по координатам и импульсам распадается на 2N независимых распределений по координатам и импульсам каждой частицы. Распределения по импульсам представляет собой полученное выше распределение Максвелла (8.). Рассмотрим более подробно распределение по координатам:

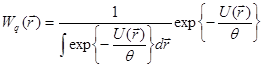(8.29)

Это распределение характеризует распределение частиц в поле произвольного потенциала .

В частности, в поле сил тяжести получаем известное барометрическое распределение:

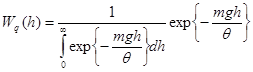(8.30)

Аналогичным образом выбирая в качестве потенциал стенок, ограничивающих объем V,

(8.31)

получаем распределение

(8.31)

Использование потенциала (8.31) и соответствующего распределения для классических систем аналогично ограничению области интегрирования по координатной составляющей фазового пространства N-кратно повторенной областью V.

Объединяя в соответствии с (8.28) распределение по координатам (8.29) и импульсам (8.23), получаем распределение по координатам и импульсам для каждой частицы:

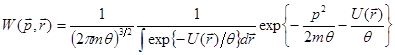(8.33)

или распределение по координатам и скоростям:

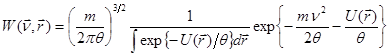(8.34)

Распределение (8.34) часто называют распределением Максвелла – Больцмана.

3.Рассмотрим общую структуру статистического интеграла. В случае отсутствия взаимодействия между частицами () статистический интеграл распадается на произведение одинаковых интегралов по переменным и для каждой частицы.

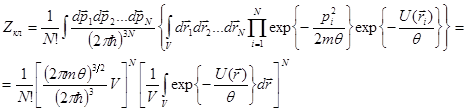
Для выделения главной асимптотики по N воспользуемся формулой Стирлинга:

т.е. ,

откуда следует

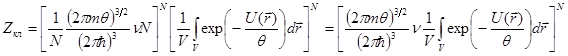(8.35)

Тогда в пространственно однородном случае в отсутствие внешних полей () и статистический интеграл принимает вид:

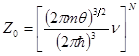(8.36)

Выражение (8.36) позволяет найти вид свободной энергии и основные термодинамические соотношения для системы классических невзаимодействующих частиц. Свободная энергия определяется из (6.13) и равна:

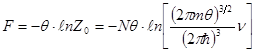(8.37)

Дальнейшее использование метода термодинамических потенциалов позволяет рассчитать основные термодинамические параметры системы, состояние которой задано параметрами ().

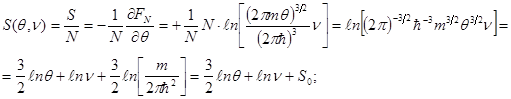(8.38)

(8.39а)

откуда следует уравнение состояния идеального газа

(8.39б)

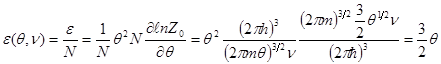(8.40)

Соответственно удельная теплоемкость равна:

(8.41)

Итак, на основе выражения статистического интеграла нами получено уравнение состояния термодинамической системы идеального газа (8.39б) и калорическое уравнение состояния этой системы (8.41).

Заметим, что соотношения (8.36)-(8.41) относятся к классическому идеальному газу, для которого справедливо условие (8.5).

Для неидеального классического газа с учетом межчастичных взаимодействий (), гамильтониан которого имеет вид получаем:

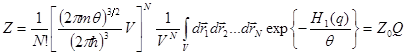(8.42)

Здесь величина Q определяется из соотношения:

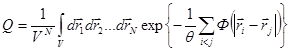(8.43)

и называется конфигурационным интегралом.

Отсюда следует, что основная проблема теоретического исследования классических неидеальных систем связана с расчетом конфигурационного интеграла Q. Заметим, что этот расчет возможен только в некоторых частных случаях на основе использования приближенных метод

 Скачать реферат