Полярные диаграммы и энергетические уровни волновых функций жесткого ротатора

4.3.8.7. Итак, нас будут интересовать s–, p–, d–, f– орбитали жесткого ротатора. Запишем соответствующие исходные функции и , с точностью до постоянного множителя:

для s-состояния и ght=57 src="images/referats/5115/image037.png">

для p- состояния и

для d- состояния и

для f- состояния и

4.3.8.8. Орбиталь s –типа – лишь одна и волновая пункция тре­бует только нормировки. Поскольку сомножитель 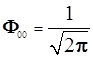уже нормирован, достаточно пронормировать функцию . Выделяя из эле­мента конфигурационного пространства (см. рис 4.3) все со­множители, определенные на переменной , получаем

и, соответственно, нормировочное соотношение имеет вид

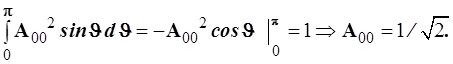(4.119)

Во всех дальнейших преобразованиях следующих двух разделов будем опускать постоянные численные коэффициенты перед волновыми функциями, получающимися в результате операций сдвигов состояний над исходными функциями – степенями синусоиды .

4.3.8.9. Квантовое число l=1 порождает три р-функции с m=1, 0, -1 т.е. орбитали с Двум из них с отвечает Нормировочный множитель находим из соотношения

.

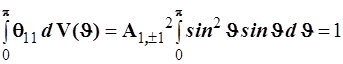Откуда следует: (4.120)

Функцию , необходимую для полного набора р-орбиталей, можно найти, сдвигая вниз или вверх на одно состояние

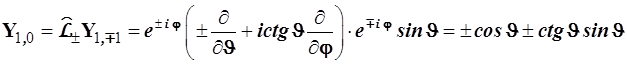
Определим нормировочный множитель для

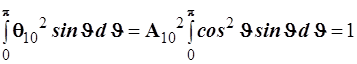
Интегрируя с помощью подстановки и, следовательно полагая, получаем

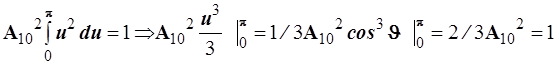, т.е.

4.3.8.10. Далее получим последовательно d-орбитали, отвечающие набору . Соответственно

(4.121)

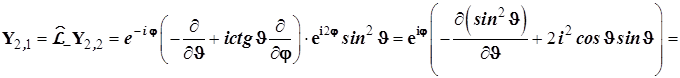
(4.121)

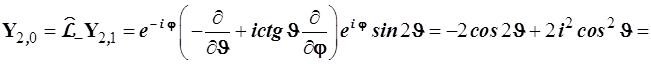
(4.122)

Отсюда получаются d-функции

; .

Величины ;; представлены в таблице 4.6.

4.3.8.11. Аналогично получается весь набор f-функций

(4.123)

Все найденные s-, р-, d- и f-орбитали сведём в таблицу 4.6.

Таблица 4.6.

Сферические волновые функции

 Скачать реферат