Понятие давления паров и теплоты

ДАВЛЕНИЯ ПАРОВ И ТЕПЛОТЫ ПАРООБРАЗОВАНИЯ ЧИСТЫХ ЖИДКОСТЕЙ

В этой работе описываются методы расчета и корреляции давления паров чистых жидкостей, а также энтальпий парообразования, поскольку их определение основывается на Р-Т данных.

Общие сведения по давлению паров

Согласно правилу фаз, давление паров чистой жидкости является однозначной функцией темпер

атуры насыщения, поэтому почти все данные о давлении паров представляют в виде зависимости

.(7.1)

Давление насыщенного пара может быть связано с любым другим интенсивным свойством насыщенной жидкости (или пара), однако температура насыщения в этом случае наиболее удобна. Если паровая фаза находится в равновесии с жидкой фазой, то условие равенства химических потенциалов, температуры и давления обеих фаз приводит к уравнению Клаузиуса-Клапейрона:

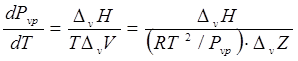(7.2)

или

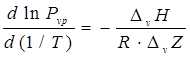.(7.3)

Большинство уравнений для расчета и корреляции давления паров получаются путем интегрирования уравнения (7.3). После интегрирования должна быть выбрана форма зависимости группы от температуры, а константа интегрирования определяется по одной точке “давление паров -температура”.

В общем случае зависимость от имеет S-образный вид. Для большинства веществ изменение наклона соответствует значению приведенной температуры =0,8-0,85. Для низкокипящих или неполярных соединений эта величина имеет более низкое значение (для метана точка перегиба =0,7), для высококипящих, а также для полярных или ассоциированных жидкостей точка перегиба перемещается в область более высоких значений Tr (для этанола – 1,0).

S-образный вид зависимости от обусловлен изменением отношения с температурой. Для нормальных жидкостей это отношение сравнительно нечувствительно к изменению температуры в диапазоне между нормальной температурой кипения вещества и его критической температурой. Объясняется это тем, что уменьшение теплоты парообразования компенсируется в некоторой степени уменьшением величины . Ниже нормальной точки кипения (при = 0,6-0,7) значение очень близко к единице и изменение отношения происходит исключительно вследствие изменения энтальпии.

Аппроксимация Р-Т данных

Для аппроксимации экспериментальных P-T данных применяются уравнения различной сложности и теоретической аргументации. Одни из них хорошо работают при температурах ниже нормальной точки кипения, другие - при более высоких температурах. Корреляции, учитывающие S-образный вид зависимости от , имеют, как правило, весьма сложную алгебраическую форму. Универсальных подходов для описания ее пока не найдено.

Выбор типа уравнения во многом зависит от объема и качества экспериментальных данных, а также от приверженности автора тем или иным подходам. Все корреляции, предложенные в настоящее время для описания P-T данных, могут быть объединены в несколько групп с весьма близкими возможностями их в каждой группе. Ниже рассмотрены методы, наиболее часто применяющиеся при массовых расчетах.

Большинство уравнений для расчета давлений паров получены интегрированием уравнения Клаузиуса-Клапейрона (7.3). Число вариантов интегрирования ограниченно. Тем не менее результаты, опубликованные в литературе, отличаются достаточно большим разнообразием. Объясняется это тем, что для достижения большей точности каждый автор обычно вводит свои поправочные коэффициенты.

В уравнении (7.3) как , так и являются функциями температуры. Величина представляет собой изменение коэффициента сжимаемости при переходе вещества из состояния насыщенной жидкости в состояние насыщенного пара.

Для прогнозирования в настоящее время довольно широко применяется уравнение Хаггенмахера

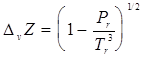,(7.4)

где при условии, что жидкость находится под давлением, равным давлению насыщенных паров.

Уравнение Хаггенмахера дает хорошие результаты при температурах, близких к нормальной точке кипения, или при более низких, чем , температурах. При уравнение Хаггенмахера следует использовать с осторожностью.

Уравнение Клапейрона

При интегрировании уравнения Клаузиуса-Клапейрона в самом простом случае предполагается, что группа имеет постоянное значение, которое не зависит от температуры.

Обозначив постоянную величину интегрирования через “A”, получим

,(7.5)

где .

Соотношение (7.5) иногда называют уравнением Клапейрона. Графически приведенная зависимость выражается прямой линией. Часто уравнение (7.5) оказывается неплохой аппроксимацией, но в общем случае оно дает существенные ошибки по причине того, что зависимость от имеет S-образный вид. Уравнение (7.5) неприменимо для температур ниже нормальной точки кипения даже для неполярных и не склонных к образованию ассоциатов веществ. Для последних линейная форма P-T зависимости может применяться для аппроксимации P-T данных только в узком температурном интервале даже в области температур, превышающих нормальную точку кипения.

Корреляция Антуана для давления паров

Антуан предложил широко используемую простую модификацию уравнения (7.5):

 Скачать реферат