Изучение зрительной трубы
Таблица 2
| № изм | Число делений изображения диагоналей ромбов | Цена дел. ок. шкалы мм | olspan=3 valign=top > Длина изображений диагоналей ромбов | Длина диагоналей ромбов | К | Кср | ||||||
| n1 | n2 | n3 | l1 | l2 | l3 | L1 | L2 | L3 | ||||
| 0,1 | ||||||||||||
Упражнение 2
Определение поля зрения оптической трубы
Для определения поля зрения трубы её фокусируют на стенную линейку с делениями и замечают. Сколько делений этой линейки видимы в трубу. Затем измеряют рулеткой расстояние от объектива трубы до линейки. Если число делений линейки, видимых в трубу, равно ![]() , а расстояние от трубы до линейки равно
, а расстояние от трубы до линейки равно ![]() , то поле зрения оптической трубы, выраженное в градусах, определяется формулой:
, то поле зрения оптической трубы, выраженное в градусах, определяется формулой: ![]() .
.
Измерения повести не менее 3-х раз и результаты занести в таблицу 3.
Таблица 3
| № | Число делений линейки, видимых в трубу n | Расстояние от трубы до линейки (см) L | а=57,3 | Аср |
| 1 2 3 |
Упражнение 3
Определение разрешающей способности оптических систем
Идеальная оптическая система, то есть такая система, которая не обладает аберрациями, согласно правилам геометрической оптики отображает каждую точку предмета (источника света) в виде точки. Идеальной оптической системой можно считать систему, в которой отображение производится параксиальными лучами. Отсюда следует, что, чем меньше отверстие системы, тем лучше должно быть изображение с точки зрения законов геометрической оптики.
Однако, как следует из теории дифракции на круглом отверстии, даже при идеальной оптической системе, то есть такой, в которой отсутствуют какие-либо аберрации, точечный источник отображается в виде кружка, угловая величина радиуса которого равна по первому дифракционному максимуму: ![]() ,
,
где ![]() –диаметр отверстия системы, а в случае линзы или зеркала (объекти ва) –диаметр входной линзы телескопа (микроскопа).
–диаметр отверстия системы, а в случае линзы или зеркала (объекти ва) –диаметр входной линзы телескопа (микроскопа).
Если два точечных источника света находятся на угловом расстоянии, y то это принимается в качестве условия предельного разрешения двух близких светящихся точек (или двух близких точечных предметов).
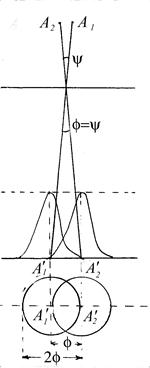
Рис. 2 .
На рис. 2 показано дифракционное изображение двух точечных источников А1 и А2, удаленных друг от друга на расстояние ![]() , даваемое идеальной линзой (зеркалом или вообще оптической системой), имеющей диаметр оправы или диафрагмы (входного зрачка)
, даваемое идеальной линзой (зеркалом или вообще оптической системой), имеющей диаметр оправы или диафрагмы (входного зрачка) ![]() . При таком расположении изображений наблюдаемых точечных источников А1 и А2, дифракционное изображение каждого из них будет иметь диаметр
. При таком расположении изображений наблюдаемых точечных источников А1 и А2, дифракционное изображение каждого из них будет иметь диаметр ![]() (рис. 2). Поэтому при выбранном условии предельного разрешения максимум интенсивности в дифракционном изображении одной точки (
(рис. 2). Поэтому при выбранном условии предельного разрешения максимум интенсивности в дифракционном изображении одной точки (![]() ) располагается над минимумом интенсивности другой точки (
) располагается над минимумом интенсивности другой точки (![]() ) и наоборот. Посредине результирующая интенсивность будет равна приблизительно 80% от интенсивности в максимуме (рис. 2). При этом наблюдатель ещё может различать два изображения. Если дальше сближать точки А1 и А2, то имевшийся между
) и наоборот. Посредине результирующая интенсивность будет равна приблизительно 80% от интенсивности в максимуме (рис. 2). При этом наблюдатель ещё может различать два изображения. Если дальше сближать точки А1 и А2, то имевшийся между ![]() и
и ![]() минимум результирующей интенсивности исчезает и оба изображения сольются в одно, то есть не будут восприниматься раздельно.
минимум результирующей интенсивности исчезает и оба изображения сольются в одно, то есть не будут восприниматься раздельно.
Таким образом, угловое расстояние между двумя светящимися объектами (точечными): ![]() или
или ![]() ,
,
является пределом разрешения данной линзы (зеркала, телескопа, сложной оптической системы). Величина обратная принимается за разрешающую силу оптической системы:
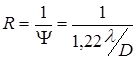 .
.
Учитывая, что максимум спектральной чувствительности глаза приходится на ![]() =5,6×10-4мм, предыдущую формулу можно записать так
=5,6×10-4мм, предыдущую формулу можно записать так
![]()
где 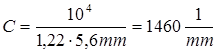 ;
;
![]() -диаметр оправы, диафрагмы, входного зрачка, линзы, выраженный
-диаметр оправы, диафрагмы, входного зрачка, линзы, выраженный
в мм.
В этом случае величина разрешающей силы указывает какое количество равноудаленных точек предмета, изображаемых линзой раздельно, приходится на единицу углового расстояния.
Другие рефераты на тему «Физика и энергетика»:
Поиск рефератов
Последние рефераты раздела
- Автоматизированные поверочные установки для расходомеров и счетчиков жидкостей
- Энергосберегающая технология применения уранина в котельных
- Проливная установка заводской метрологической лаборатории
- Источники радиации
- Исследование особенностей граничного трения ротационным вискозиметром
- Исследование вольт-фарадных характеристик многослойных структур на кремниевой подложке
- Емкость резкого p-n перехода
