Линейные электрические цепи постоянного и синусоидального тока

Найдем контурные токи:

I11 = D11/D = 1 A; I22 = D22/D = 3 A

Теперь посчитаем токи во всех ветвях.

I1= J1 = 1 A

I2= I22 – J1= 2 A

I3 = I22 – I11 = 2 A

I4 = – I22= -3 A

I6 = I11 – J1 = 0 A

I7 = I11 = 1 A

· Теория, метод узловых потенциалов

Возьмём для примера ПЭС изображённую на рисунке 2.В изображённой цепи есть 3 узла. Так как любая(одна) точка схемы може

т быть заземлена без изменения токораспределения в ней, один из узлов схемы можно заземлить, то есть принять потенциал равным 0. Заземлим узел с потенциалом . По первому закону Кирхгофа для двух оставшихся узлов запишем систему уравнений:

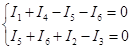
Затем воспользуемся обобщённым законом Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов на концах участка цепи и имеющейся на этом участке ЭДС E. По обобщенному закону Ома, запишем систему:

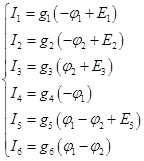
Подставим в и сгруппируем слагаемые с одинаковыми потенциалами:

– это и есть уравнения по МУП.

Уравнения имеют следующую структуру. Потенциал узла умножается на его собственную проводимость – сумма проводимостей всех ветвей, сходящихся к узлу. Из этого произведения вычтем потенциалы узлов, имеющие с рассматриваемым общие ветви, умножаем на взаимную проводимость этих узлов (сумму проводимостей всех ветвей, которые находятся между этими двумя узлами). Потенциал узла, потенциал который мы приняли равным нулю, в уравнения не входит. Матрица в общем случае будет симметрична, на главной диагонали будут стоять собственные проводимости узлов; эти элементы матрицы всегда будут иметь знак «плюс». Недиагональные элементы всегда будут иметь знак «минус». В правой части уравнений – записывается алгебраическая сумма произведений источников ЭДС на проводимости соответствующих ветвей, причем это произведение берется со знаком «+», если ЭДС направлена к узлу, и со знаком «–», если от узла.

Теперь рассмотрим случай, когда в цепи будут присутствовать источники тока (рис 3). Проводимость первой ветви в этом случае будет равняться нулю, и первое уравнение будет выглядеть следующим образом:

,

источник тока вписываем в правую часть со знаком «плюс», если он направлен к узлу и со знаком «минус» в противоположном случае. Количество уравнений не уменьшается, так как уравнения по

МУП не зависят от изначально выбранных направлений токов в ветвях. Количество уравнений по МУП рассчитываются по формуле:

.

Докажем правильность расстановки знаков, обратившись к стандартной ветви (рис 4). Рассмотрим схему, содержащую узлов, и рассмотрим стандартную ветвь, сначала без источника тока.

Здесь:

.

Значит

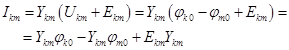
Для любого узла выполняется первый закон Кирхгофа (выбрасываем только собственный узел).

.

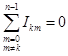Учитываем, что узел к узлу никакого отношения не имеет, его можно вынести за скобку:

.

Отсюда

,

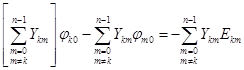сумма проводимостей всех ветвей, сходящихся к узлу, умноженная на потенциал собственного узла, взятая со знаком «плюс», минус сумма произведений проводимостей между i-м и j-м узлом и потенциалов соответствующих узлов равна взятой со знаком «минус» сумме произведений источников на проводимости.

Теперь включим источник тока (рис 5). В данном случае он будет вытекающим. С учетом его наличия, уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

.

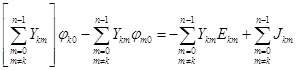Полученный результат также соответствует результату, полученному ранее для частного примера.

Если мы теперь посмотрим на уравнение

,

где в могут входить как источники тока, так и источники ЭДС, умноженные на проводимость, – собственные проводимости, берутся со знаком «+», – взаимные проводимости, берутся со знаком «–».

Получим эту же систему уравнений в стандартном виде, т.е. через стандартную ветвь. Для стандартной ветви:

.

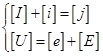Опираясь на закон Ома и записанные выше уравнения, получим:

.

Вспомним про редуцированную матрицу инциденций, умножим правую и левую часть на :

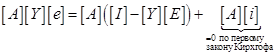
Сравниваем число уравнений и число неизвестных. Матрица дает нам N-1 уравнений, а число неизвестных – это число ветвей графа. Вспоминаем, что

Подставляем это в полученное ранее выражение:

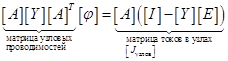
Свели уравнение к полному. Получаем относительно :

Теперь можем найти все необходимое:

,

Замечание: Матрица

 Скачать реферат

Страница:  1  2  3  4 

Другие рефераты на тему «Физика и энергетика»:

• Автоматизация энергоблока АЭС с ВВЭР-1000
• Физические основы электронных устройств
• Электроснабжение предприятия по производству деталей к автомобилям
• Установка освещения на птицефабрике
• Изучение вращательного движения на приборе Обербека. Упругие и неупругие удары шаров