Методика реализации межпредметных и внутрипредметных связей при обучении математике

В учебном курсе понятия могут играть разную роль: одни из них являются общими, с широким спектром приложений, другие же играют функцию подчиненную. Учитель должен уметь выделять общие, ведущие понятия курса. Ведущими понятиями будем считать те, которые удовлетворяют следующим критериям: они должны формировать научное мировоззрение; значительно чаще других понятий служить средством изучения разл

ичных вопросов математики; активно работать на протяжении большого промежутка времени; способствовать наиболее полной реализации внутрипредметных связей, а, в конечном счете, и межпредметных; иметь прикладную и практическую направленность. Примерами таких ведущих понятий могут служить: число, величина, фигура, функция, график, уравнение, неравенство, равносильность, алгоритм и т. д.

Выделив ведущие понятия, учитель должен затем проследить их развитие во всем курсе школьной математики, тем самым определить его содержательно-методические линии, которые обеспечивают курсу необходимую систематичность и последовательность, отражают идейную сторону математики и являются важнейшим средством обеспечения преемственности всего изучаемого материала.

Перечислим основные содержательно-методические линии школьного курса алгебры: числовая, алгоритмическая, функциональная, линия уравнений и неравенств.

Реализация внутрипредметных связей вовсе не должна означать установление искусственных связей; наряду со связями, играющими положительную роль в процессе обучения, имеют место и связи отрицательного действия. Задача учителя — суметь в каждом конкретном случае отчленить одни связи от других и исключить связи отрицательного воздействия. Приведем примеры связей отрицательного действия.

1. Учащиеся, используя основное свойство дроби, ошибочно преобразуют дробь к следующему виду: или .

Ошибки получены в результате сокращения дроби не на множитель, как того требует основное свойство дроби, а на слагаемое.

2. При введении понятия иррационального числа многие учителя иллюстрируют это понятие лишь такими примерами: ; - и т. д. Это приводит к тому, что затем на вопрос: «Приведите примеры иррациональных чисел» — учащиеся отвечают лишь подобными примерами, тем самым происходит сужение объема понятия иррационального числа. Этого не произошло, если бы народу с приведенными выше примерами учитель показал и иррациональное число 0,001 00001 . (используется связь с бесконечными непериодическими десятичными дробями).[7]

Значительная часть приведенных ошибок возникла в результате следующих причин. Это большая прочность ранее образованных связей по сравнению с позже возникающими; стремление учащихся к автоматическому применению теории без достаточного анализа возможности ее применения; доминирование ассоциативных связей над смысловыми, склонность действовать по стереотипу.

Отрицательные связи, устанавливаемые учениками, можно предвидеть и вести работу, которая могла бы их предотвратить. Так, например, большое число решенных задач по разложению на множители трехчленов вида x2+px + q не облегчает, а скорее затрудняет формирование навыка разложения на множители трехчленов вида ах2+bх+с (учащиеся записывают ошибочный ответ в виде (х — х1)(х — х2), опуская множитель а). Поэтому выполнение упражнений по разложению на множители трехчленов первого вида не должно быть длительным. Преподавание должно вестись по способу чередования разнотипных задач.

Одни и те же понятия могут быть определены на основе разных исходных посылок, различными способами. Все эти определения могут оказаться равноценными, но они будут иметь существенную разницу в достигнутых результатах обучения, в частности будет различной полнота внутрипредметных связей. Задача состоит в том, чтобы отыскать такой вариант, при котором эти результаты обучения будут наилучшими. Важно разъяснять учащимся реальный смысл понятий, показывать, отражением каких сторон действительности они являются.

Остановимся в связи с этим на теме «Действительные числа». Хотя данная тема служит основой изучения вопросов математического анализа, она, слабо усваивается учащимися. В первую очередь отметим, что школьники не видят связей между понятием действительного числа и понятиями математического анализа, изучаемыми в школьном курсе. Одна из причин — выведение понятия действительного числа из задачи об извлечении корня.

Это задача курса алгебры, а не математического анализа. Вопрос об извлечении корня не является главным в данном случае. Его целесообразно использовать лишь для мотивировки введения новых чисел — иррациональных.

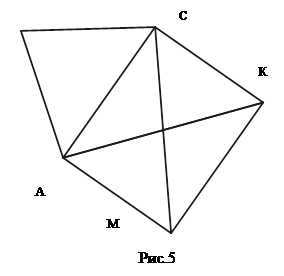
Действительно, после того как будет доказано, что нет рационального числа, квадрат которого равен 2, учащимся можно предложить задачу: «Постройте квадрат ABCD со стороной 1 и на диагонали АС этого квадрата постройте другой квадрат (рис.5). Чему равна площадь получившегося квадрата АСКМ?»

Так как SABCD = 1 ед.2, то SACD= ед.2.

Так как DACD = DCDK= DKDM= DADM, то Sackm = Sacd + ScDk + SKdm + + Sadm= =2 ед.2. Если сторону квадрата АСКМ (диагональ АС) обозначить через х, то получим х2=2. Но раз мы реально имеем квадрат площадью 2 ед.2, то должно существовать и число, квадрат которого равен 2.

Для математического анализа ведущим является расширение множества рациональных чисел до множества действительных чисел, которое является непрерывным (вместе с этим решается вопрос и об извлечении корня из положительного числа). Главенствующее значение действительных чисел в курсе математического анализа как раз и состоит в том, что они способны выразить непрерывное изменение величины. (В случае доминанты задачи об извлечении корня этот вопрос остается скрытым.)

Таким образом, отработка понятия действительного числа и понятия непрерывной величины — это две стороны одного и того же процесса. Так как наглядной иллюстрацией непрерывного процесса служит движение точки по прямой, то в основе формирования понятия действительного числа должно быть, в первую очередь, понятие прямой, совокупность точек которой такова же по своей структуре, как и множество действительных чисел. Рассматривая так действительные числа, можно осуществить преемственность данной темы с такими вопросами анализа, как предел, непрерывность, производная, интеграл и т. д. [7]

Важным требованием к определению понятия является его согласование с естественно-интуитивным представлением о нем. Не может, например, считаться целесообразным определение целого числа через класс пар натуральных чисел, ибо оно не сформирует у учащихся тех умений и навыков, которыми они должны владеть для проведения числовых и алгебраических преобразований. Это же следует сказать и о таких определениях: определение натурального числа как класса эквивалентных множеств; определение рационального, числа как класса пар целых чисел; определение вектора как параллельного переноса; определение функции как множества пар с различными первыми компонентами. Несоответствие между интуитивным представлением о понятии вектора и его формальным определением можно преодолеть за счет введения понятия вектора через направленный отрезок, а функции через физический прототип — переменную величину.[3]

 Скачать реферат