Методика реализации межпредметных и внутрипредметных связей при обучении математике

Фактически это следует из разложения функции в ряд Тейлора. Действительно, пусть мы имеем разложение

Если бы функция f(x) в точке x0 обладала лишь свойством непрерывности в точке x0, то мы имели бы приближённое равенство f(x)»f(x0).

Если же функция f(x) в точке x0 имеет первую производную, то приближение будет более т

очным; к правой части равенства f(x)=f(x0) добавится ещё одно слагаемое

т.е. имеет место приближённое равенство:

При наличии второй производной функции f(x) в точке х0 будем иметь

Следовательно, если функция бесконечно дифференцируема, то приближение может быть сделано с любой степенью точности.

Однако в курсе алгебры и начал анализа рассматривается лишь понятие первой производной. Поэтому при изучении применений производной к приближённым вычислениям ограничиваются лишь двумя первыми слагаемыми ряда Тейлора, т.е. используют приближённое равенство:

Обобщение формулы

на уровне идеи аппроксимации даёт представление о решении этих вопросов. Если функция имеет производные любого порядка, то её можно приблизить многочленом с какой угодно точностью. Так получаются ряды для функций

sin х , cos x , е х , 1n x .

Геометрически это означает, что график функции n-раз, дифференцируемой в точке х0, вблизи этой точки можно приближённо считать графиком некоторого многочлена n-ой степени.

Конечно, в школьном курсе нет возможности рассматривать с учащимися этот вопрос в таком общем плане. Но внимание к постановке задачи, отдельные примеры не только расширяют кругозор учащихся, но и помогут преодолеть некоторые методические трудности.

Одной из таких трудностей, как показал опыт, является переход от равенства

к равенству

Возникновение этой трудности можно предотвратить уже при постановке проблемы, если начать изложение примерно таким пояснением: «Вы знаете, что для функции f(x), непрерывной в точке х0, выполняется равенство

С другой стороны, если функция в некоторой точке х0 имеет предел, то её значения вблизи х0 приближённо равны этому пределу, т.е. для х»х0.

Отсюда следует, что для непрерывной в х0 функции её значения вблизи х0 можно приближённо вычислять по формуле f(x)=f(xo).

то теперь вывод формулы получается без особого труда: так как

то для Dх»0 выполняется равенство

отсюда

Такой подход к обобщению материала по применению производной к приближённым вычислениям позволяет представить перед учащимися формулу

f ( х 0 + Dх) » f ( х 0 ) + f ' ( х 0 ) D х

как частный случай решения общей задачи приближения функции многочленом, что даёт заменять сложные вычисления простыми.

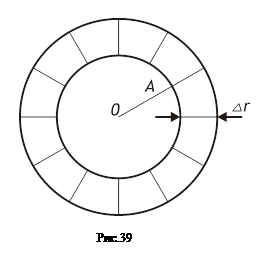
Для наглядности иллюстрации формулы можно использовать геометрические примеры.

Рассматриваем приращение площади круга (рис. 39). Пусть радиус круга ОА=r.

Тогда площадь его, как функция радиуса, выражается формулой S(r)=pr2.

Дав радиусу приращение Dr, можем заметить, что DS(r)~2prDr, т.е. площадь заштрихованного кольца приближённо равна произведению длины окружности радиуса г на ширину кольца (приращение Dr).

Множитель 2pr, стоящий в правой части равенства, есть производная функции S(r), так как S'(r)=2pr. Мы снова имеем формулу DS(r)»S'(r)Dr. Чем тоньше кольцо, т.е. чем меньше Dr, тем меньше будет погрешность при замене площади кольца выражением 2prDr.

Если учащиеся усвоят, что формула f(x0+Dx)=f(х0)+f(х0)Dх даёт возможность приблизить всякую дифференцируемую функцию некоторой линейной, то это даст возможность разъяснить не только получение уравнения касательной.

Традиционно касательную трактуют как предельное положение секущей. Однако остаётся вне поля зрения важнейшее свойство касательной: касательная из всех прямых, проходящих через точку с абсциссой х0, теснее всех прилегает к кривой. Такая трактовка сразу же позволяет использовать формулу f(х0+Dх)»f(х0)+f(х0)Dх. Касательной к графику функции y=f(x) в точке х0 является график той линейной функции, которая приближает f(x).[8]

Рассмотрев эту приближённую формулу, при изучении вопроса о касательной к графику функции учащимся целесообразно сообщить, что геометрический смысл этой формулы состоит в том, что ордината точки графика функции f(x) заменяется ординатой соответствующей точки касательной.

Проиллюстрируем формулу f(x0+Dx)»f(x0)+f(х0)Dх несколькими примерами.

Известно, что значение синуса для достаточно малых значений аргумента приближённо равно значению аргумента. Это свойство связано с только что рассмотренным геометрическим смыслом приближённой формулы f(х0+Dх)»f(х0)+f(х0)Dх.

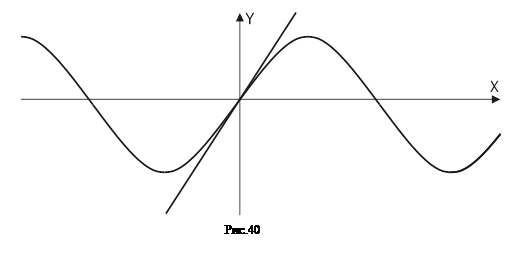
Действительно, построив график функции y=sinx и проведя касательную к этому графику в точке (0;0) (рис.40), мы замечаем, что ею будет служить прямая у=х. И тогда при вычислении значений синуса малых углов мы заменяем искомую ординату точки графика y=sinx ординатой соответствующей точки касательной, а так как касательная есть у=х, то искомое значение синуса мы заменяем соответствующим значением аргумента. Так, вычисляя значения синуса для угла в один градус, мы, переводя градусы в радианы, будем иметь: sin l°»sin 0,017-0,017.

Подобную картину мы наблюдаем и в случае вычисления для малых углов значений тангенса. В точке (0;0) касательной к графику функции тангенса будет прямая у=х (в этом можно убедиться, подставив в формулу уравнения касательной y=y0+f (х0)(х-х0) необходимые значения у0, х0, f(x0) для функции y=tg х.)

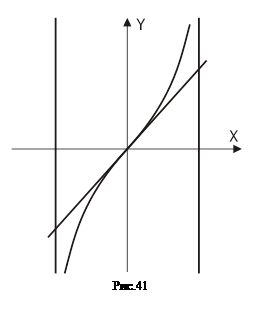
Тогда вычисляя значения тангенса для малых углов, мы приближённо заменяем эти значения, значениями аргумента, выразив их предварительно в радианах.

Последние два примера могут быть использованы учителем при изучении производных тригонометрических функций.

Замечание 1. Для приближённого равенства sinx=x характерно то, что для малых положительных значений аргумента х значения синуса подсчитаны с избытком. На рисунке 40 график функции y=sinx расположен для х>0 ниже прямой у=х.

Замечание 2. В случае тангенса его значения для малых положительных углов подсчитываются с недостатком. На рисунке 41 график y=tg x расположен для х>0 выше прямой у=х.

Обобщающее повторение на уровне теорий непосредственно освещает полученные знания не только в плане внутрипредметных связей, но и межпредметных, так как многие понятия различных учебных предметов получают единую трактовку с позиции одной какой-нибудь теории. На уровне теорий обобщающее повторение вызывает у школьников широкие межсистемные ассоциации, что позволяет им осуществлять систематизированный перенос знаний из одного учебного предмета в другой.

 Скачать реферат