Формирование логической грамотности при обучении математике младших школьников

Задача 15. Сумма четырех различных чисел равна 13. Наименьшее из этих чисел на 5 меньше наибольшего. Найди эти числа.

Сначала ученики выполняют чертеж (рис. 5).

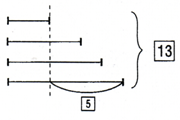
Рис.5

Затем учащиеся пытаются преобразовать чертеж, чтобы получить одинаковые числа, как они делали в предыдущих задачах. Ученики приходят к выводу, что

этого сделать нельзя, так как в условии ничего не говорится о числовых отношениях между вторым и третьим числом. Встает проблема: можно ли решить эту задачу? Может быть, в ней не хватает данных? Учитель предлагает использовать для решения этой задачи способ подбора.

Рассуждения удобнее начать с наименьшего из чисел.

— Пробуем число 0. Тогда получаем: 0+ □ + □ + 5 = 13. Подберем пропущенные числа. Их сумма равна 13 - 5 - 0 = 8. Эти числа должны быть разными и быть больше 0, но меньше 5. Между 0 и 5 идут числа 1, 2, 3, 4. Среди них нельзя выбрать два разных числа, дающих в сумме 8. Значит, число 0 не подходит.

Пробуем число 1. Тогда получаем: l + □+ □+ 6 = 13. Подбираем пропущенные числа. Их сумма равна: 13-1-6 = 6. Между числами 1 и 6 стоят числа 2, 3, 4, 5. Среди них выбираем два, дающих в сумме 6. Это числа 2 и 4. Проверяем, правильно ли мы нашли четыре числа. Для этого складываем их: 1 + 2 + 4 + 6 = 13. Получили сумму, данную в задаче. Другие условия также соблюдены: числа различные, наименьшее из этих чисел 1, оно на 5 меньше наибольшего числа 6.

Получив один ответ, нужно проверить, нет ли других вариантов ответа. Для этого пробуем число 2. Тогда получаем: 2 + □ + □ + 7 = 13. Подбираем пропущенные числа. Их сумма равна 4. Среди чисел 3, 4, 5, 6 нельзя выбрать два числа, дающих в сумме 4 (сумма любых двух перечисленных чисел больше 4). Можно проверить число 3 таким же образом. Числа, начиная с 4, проверять не нужно, так как сумма двух чисел получается равной или больше: 13 : 4 + □ + □ + 9 = 13.

Получаем ответ задачи: числа 1, 2, 4, 6.

В итоге важно подчеркнуть, что задачу решили, подбирая нужные числа. Делали это так: последовательно рассматривали различные возможные варианты и выбрали те, которые соответствуют всем условиям задачи. Чертеж помогал выделить эти условия из текста задачи. В некоторых случаях перебор удобно начинать не с наименьшего, а с наибольшего возможного числа. Иногда, оценив полученный результат, можно пропустить некоторые числа. Этот способ удобно использовать, когда число возможных вариантов небольшое.

При решении следующих задач ученики упражняются в применении способа подбора.

Задача 16. Сумма трех разных двузначных чисел равна 34. Какие это числа? (10,11,13)

Задача 17. Трое ребят были на рыбалке. Вместе они поймали 14 рыб. Андрей поймал меньше всех рыб. Дима поймал в 3 раза больше рыб, чем Вова. Сколько рыб поймал каждый мальчик? (Вова поймал 3 рыбы, Дима поймал 9 рыб, Андрей поймал 2 рыбы.)

Задача 18. Внучке, маме и бабушке вместе 114 лет. Сколько лет в отдельности внучке, маме и бабушке, если возраст каждой выражается двузначным числом, оканчивающимся одной и той же цифрой? (Внучке 18 лет, маме 38 лет, бабушке 58 лет.)

Серия VI

В задачах серии VI выводится следующая рекомендация при решении нестандартных задач: полезно переформулировать задачу, т.е. сказать ее другими словами, чтобы она стала знакомой и понятной. При этом в большинстве случаев будет происходить перевод текста задачи на язык математики.

Задача 19. Число яблок в корзине двузначное. Эти яблоки можно раздать поровну 2, 3 или 5 детям, но нельзя раздать поровну 4 детям. Сколько яблок в корзине? (Укажите такое наименьшее двузначное число.)

Сначала ученики пытаются сделать рисунок или чертеж к задаче, но испытывают затруднения, так как на чертеже трудно показать, что нельзя раздать яблоки поровну 4 детям, следовательно, непонятно, как использовать чертеж для решения задачи. Тогда ученики начинают применять способ подбора. Учитель предлагает сначала изменить формулировку задачи, чтобы легче было выполнить перебор. Выясняется, что если яблоки можно раздать поровну 2, 3 и 5 детям, значит, число яблок делится на 2, 3. 5. Если яблоки нельзя раздать 4 детям поровну, значит, число яблок не делится на 4. Задачу переформулируют следующим образом: «Найди наименьшее двузначное число, которое делится на 2, 3,5 и не делится на 4».

Далее выполняется перебор. Ученики проверяют наименьшее двузначное число 10. Оно делится на 2 и 5, но не делится на 3, значит, число 10 не подходит. Перебор можно сократить, не рассматривать все числа подряд, а проверять только числа, делящиеся на 5. Число 15 не подходит, так как не делится на 2. Так ученики доходят до числа 30, которое делится на 2, 3, 5 и не делится на 4. Значит, в корзине 30 яблок.

Данную задачу можно было бы решить, выполняя чертеж. Начертить в тетради луч и откладывать на нем последовательно отрезки длиной 2, 3, 5 клеточек, найти точку, в которой соединяются концы отрезков трех видов, подсчитать число клеток от начала луча до этой точки. На чертеже следовало бы проверить, что отрезки длиной 4 клеточки не укладываются целое число раз в большом отрезке длиной 30 клеток. И только тогда назвать ответ задачи. Этот способ трудоемкий, но он может оказаться более легким для некоторых учеников в силу их индивидуальных особенностей.

В следующих задачах используется прием переформулирования задачи, а затем они решаются известными учащимся способами.

Задача 20. Если конфеты раскладывать по 2, 3, 4, то всегда остается 1 лишняя конфета. А если их раскладывать по 5, то лишних конфет нет. Сколько конфет, если их меньше 50? (25 конфет.)

Задача 21. В детском саду 100 детей. Для каждого ребенка купили альбом, краски, кисточку. Продавец выписал чек на 3 750 рублей. Докажи, что при подсчете общей стоимости покупки допущена ошибка, если цены предметов выражались целым числом рублей. (Для нахождения общей стоимости цену набора надо умножить на 100, поэтому в результате должно получиться число, оканчивающееся двумя нулями, а число 3 750 оканчивается одним нулем.)

Серия VII

В задачах серии VII выводится следующая рекомендация при решении нестандартных задач: условие или вопрос задачи можно разделить на части и решить задачу по частям.

Задача 22. В два автобуса сели 123 экскурсанта. Затем из одного автобуса вышли 8 человек. Трое из них сели в другой автобус, а остальные поехали на машине. После этого в автобусах стало пассажиров поровну. Сколько пассажиров было в каждом автобусе сначала?

По усвоенной первой рекомендации ученики вначале делают к задаче чертеж (рис. 6).

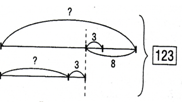
Рис. 6

Учитель предлагает решать эту задачу, разбив ее на части, чтобы облегчить решение. Ученики читают первые три предложения из текста задачи и думают, что по этим данным можно узнать.

1)8-3 = 5 (чел.) — поехали на машине.

2) 123 - 5 = 118 (чел.) — остались в каждом автобусе.