Разработка элективного курса по теме: "Кривые второго порядка" для учащихся старшей школы

Греческие учёные создали теорию конических сечений – кривых второго порядка, имеющих особенно большое значение в науке и технике. Открытие их приписывается Менехму (4 век до н.э.), ученику Евдокса Книдского и, как полагают, учителю Александра Македонского. Менехм определял эти кривые как сечения конуса плоскостью, перпендикулярной к его образующей.

Что послужило поводом к этому открытию? Мо

жет быть, поиски решения знаменитой делосской задачи об удвоении куба, может быть практический вопрос о том, насколько должен быть вытянут овал, находящийся в качестве архитектурного сооружения на фронтоне здания, чтобы с известного места перед зданием он казался кругом.

Есть данные полагать, что Менехм знал свойства параболы и гиперболы, выражаемые в наши дни равенствами y2=2px и xy=c, и использовал эти свойства для делосской задачи удвоения куба. К сожалению, это первое сочинение по теории конических сечений было утеряно. Также не дошла до нас работа греческого геометра Аристея, написавшего пять книг о пространственных местах», из которых много заимствовал Евклид для своей (также утраченной) работы о конических сечениях.

Архимед решил задачу о квадратуре сегмента параболы. Сравнивая фигуры, вписанные в эллипс и в окружность, построенную на большой оси эллипса как на диаметре, он определил и площадь эллипса.

Однако все сведения о конических сечениях были ещё разрозненны. Первая методическая обработка конических сечений принадлежит Аполлонию Пергскому (3 – 2 в. до н.э.). Это был трактат «О конических сечениях». В своём трактате Аполлоний систематизировал всё, что было известно до него, и открыл ряд важных свойств, установил их названия.

К кривым второго порядка математическая наука обратилась только в 17 веке, в связи с созданием аналитической геометрии.

Способы образования кривых второго порядка

Исследование особенностей формы кривой второго порядка и её свойств средствами дифференциальной геометрии возможно, когда кривая выражена в аналитической форме, т.е. уравнением. Однако, прежде чем исследовать уравнение кривой, необходимо его составить на основании некоторых данных. Для этого надо рассмотреть способы образования кривых.

1. Кривая определяется как линия пересечения данной поверхности плоскостью, положение которой определено.

В истории развития учения о кривых этот способ является первым. Греки определяли кривые второго порядка как сечения кругового конуса. Таково же происхождение кривых Персея, получаемых в результате сечений плоскостью поверхности тора. Эвольвента круга может быть определена как линия пересечения поверхности касательных к винтовой линии, перпендикулярной к её оси и т.д.

2. Кривая определяется как геометрическое место точек, обладающих данным свойством.

Этот способ особенно употребителен. Он широко практиковался ещё греческими математиками; так Евклид рассматривал конические сечения как геометрические места точек, сохраняющих постоянное отношение расстояний от данной точки и от данной прямой. Как геометрическое место точек была определена Диоклесом его циссоида. Таким же способом определяет Никомед конхоиду. Такие линии, как овалы Декарта, овалы Кассини, улитка Паскаля, строфоида, верзиера и целый ряд других кривых, определяются обычно как геометрические места.

3. Кривая определяется как траектория точки, характер движения которой обусловлен тем или иным образом.

4. Кривая определяется как линия, получаемая в результате того или иного геометрического преобразования уже известной кривой.

Этот способ образования кривых является наиболее эффективным. Он не только даёт неиссякаемые средства для определения новых кривых, но и позволяет определять свойства но вой кривой как отражение свойств преобразуемой кривой.

Мы заключим обзор различных способов, дающих средства для аналитического определения кривых, ещё одним, естественным по сравнению с предыдущими, в том смысле, что составлять уравнение кривой в том смысле уже не приходится, так как кривая задаётся сразу же в аналитической форме и представляет собой график той или иной функции и их уравнений.

3. Эллипс.

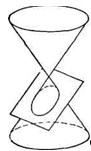
Рис. 5

Эллипс

Определение. Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек F1 и F2 этой плоскости, называемых фокусами, есть величина постоянная.

При этом не исключается совпадение фокусов эллипса. Очевидно, если фокусы совпадают, то эллипс представляет собой окружность.

Для вывода канонического уравнения эллипса выберем начало О декартовой системы координат в середине отрезка F1F2, а оси Ох и Оу направим так, как указано на рис. 6 (если фокусы F1 и F2 совпадают, то О совпадает с F1 и F2, а за ось Ох можно взять любую ось, проходящую через О).

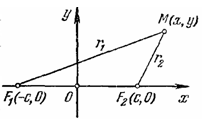
Рис. 6

Пусть длина отрезка F1 F2 равна 2с. Тогда в выбранной системе координат точки F1 и F2 соответственно имеют координаты (-с, 0) и (с, 0). Обозначим через 2а постоянную, о которой говорится в определении эллипса. Очевидно, 2а>2с, т. е. a>с (Если М - точка эллипса (см. рис. 6.2), то |MF1| + |MF2| = 2a, а так как сумма двух сторон MF1 и MF2 треугольника MF1F2 больше третьей стороны F1F2=2c, то 2а>2с.) Случай 2а=2с естественно исключить, так как тогда точка М располагается на отрезке F1F2 и эллипс вырождается в отрезок.). Пусть М - точка плоскости с координатами (х, у) (рис. 6.2). Обозначим через r1 и r2 расстояния от точки М до точек F1 и F2 соответственно. Согласно определению эллипса равенство

r1+r2=2а(1.1)

является необходимым и достаточным условием расположения точки М (х, у) на данном эллипсе.

Используя формулу расстояния между двумя точками получим

(1.2)

Из (6.1) и (6.2) вытекает, что соотношение

(1.3)

представляет собой необходимое и достаточное условие расположения точки М с координатами х и у на данном эллипсе. Поэтому соотношение (1.3) можно рассматривать как уравнение эллипса. Путем стандартного приема «уничтожения радикалов» это уравнение приводится к виду

(1.4)

Где b2=a2-c2(1.5)

Так как уравнение (1.4) представляет собой алгебраическое следствие уравнения эллипса (1.3), то координаты х и у любой точки М эллипса будут удовлетворять и уравнению (1.4). Поскольку при алгебраических преобразованиях, связанных с избавлением от радикалов, могли появиться «лишние корни», мы должны убедиться в том, что любая точка М, координаты которой удовлетворяют уравнению (1.4), располагается на данном эллипсе. Для этого, очевидно, достаточно доказать, что величины r1 и r2 для каждой точки удовлетворяют соотношению (1.1). Итак, пусть координаты х и у точки М удовлетворяют уравнению (1.4). Подставляя значение у2 из (1.4) в правую часть выражения (1.2) для r1 после несложных преобразований найдем, что