Разработка элективного курса по теме: "Кривые второго порядка" для учащихся старшей школы
Если центр эллипса находится не в начале координат, но его оси параллельны координатным осям, то он задаётся уравнением ![]() (4), где С (а; b) – центр эллипса. Это легко следует из формул параллельного переноса, или каноническим уравнением
(4), где С (а; b) – центр эллипса. Это легко следует из формул параллельного переноса, или каноническим уравнением
![]() (5) – С (х; у) – центр элл
(5) – С (х; у) – центр элл
ипса.
Данного материала достаточно для построения эллипса в том случае, если он задан уравнением, содержащем как квадраты, так и первые степени переменных.
б) Построить график ![]()
I способ
Преобразуем к виду (4): 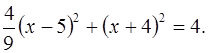
Это уравнение эллипса с центром в точке С (5; – 4), где k = 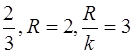 (рис. 28)
(рис. 28)
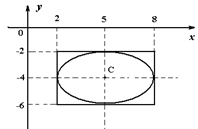
Рис. 28
II способ
Преобразуем к виду (5): ![]() . Получили уравнение эллипса с центром в точке С (5; – 4), где а = 3, b = 2.
. Получили уравнение эллипса с центром в точке С (5; – 4), где а = 3, b = 2.
Строим сам эллипс.
2. Найти длины полуосей и координаты фокусов следующих эллипсов:
а) ![]()
Приводим уравнение к каноническому виду ![]() , а = 3, b = 2.
, а = 3, b = 2.
Фокусы F1 и F2 имеют координаты F1(с; 0) и F2(– с; 0).
![]()
Итак, F1(![]() ; 0) и F2(
; 0) и F2(![]() ; 0) а = 3, b = 2.
; 0) а = 3, b = 2.
б) ![]()
Решаем аналогично а). 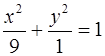 , а = 3, b = 1.
, а = 3, b = 1.
F1(с; 0), F2(– с; 0). ![]()
Итак, F1(![]() ; 0) и F2(
; 0) и F2(![]() ; 0) а = 3, b = 1.
; 0) а = 3, b = 1.
в) ![]()
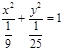 , а =
, а = ![]() , b =
, b = ![]() .
.
F1(с; 0), F2(– с; 0): ![]()
Итак, а = ![]() , b =
, b = ![]() , F1(
, F1(![]() ; 0), F2(-
; 0), F2(-![]() ; 0).
; 0).
3. Найти координаты точек М, принадлежащих эллипсу 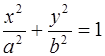 и равноудалённых от фокусов.
и равноудалённых от фокусов.
Пусть М (х; у), тогда МF1 = МF2 (по условию). Т. к. F1(с; 0), F2(– с; 0): ![]() то
то ![]()
![]()
Если х = 0, то, подставляя его в исходное уравнение, получим: ![]() ,
, ![]() Следовательно,
Следовательно, ![]() и
и ![]() .
.
4. Взяв на плоскости прямоугольную декартову систему координат, изобразить области, определяемые следующими системами неравенств.
а) 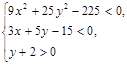
Построим множество точек, определяемых 1-м, 2-м, 3-м неравенством.
Найдём пересечение этих множеств.
I. Построим эллипс ![]() но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.
но т. к. неравенство строгое, то точки эллипса не принадлежат искомой области, т.е. неравенство (2) задаёт внутренние точки эллипса.
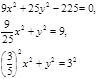
Устанавливаем, что R = 3, 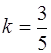 (0< k <1),
(0< k <1), 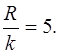 Cтроим осевой прямоугольник со сторонами
Cтроим осевой прямоугольник со сторонами 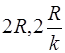 и изображаем эллипс.
и изображаем эллипс.
II. Строим множество точек, заданных вторым неравенством. Для этого строим прямую 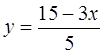 и штрихуем определяемую область.
и штрихуем определяемую область.
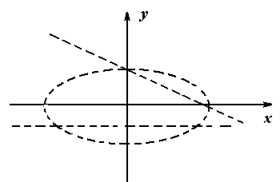
Рис. 29
III. Аналогичные рассуждения для построения области, заданной неравенством у + 2 > 0.
Построение.
б) 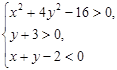
Построим множество точек, определяемых 1-м, 2-м, и 3-м неравенствами.
Найдём пересечение этих множеств.
I. ![]() – эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду
– эллипс, точки которого не принадлежат искомой области (неравенство строгое), т.е. неравенство задаёт внешние точки эллипса. Приведём уравнение к каноническому виду
![]()
Строим осевой прямоугольник со сторонами a и b, изображаем эллипс.
II. Строим множество точек, заданных неравенством (2). Для этого изображаем прямую у = 3 и штрихуем определяемую область.
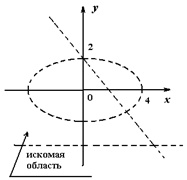
Рис. 30
5. Определить вид и расположение кривой ![]()
Решение. Дополним члены, содержащие х и у соответственно, до полных квадратов:
![]()
Отсюда получаем
![]()
Следовательно, кривая, заданная исходным уравнением, представляет собой эллипс с полуосями![]()
Центр эллипса находится в точке ![]() .
.
Задачи для самостоятельного решения
1. Написать каноническое уравнение эллипса, длина малой оси которого равна 6, а фокусное расстояние равно 8.
2. Написать каноническое уравнение эллипса, если известно, что расстояние между концами большой и малой оси равно 5, а сумма длин полуосей равна 7.
3. Написать каноническое уравнение эллипса, если расстояния фокуса его от концов большой оси равны 2 и 18.
3.2 Материал для закрепления теме гипербола
Упражнения:
Упражнение 1: Сформулируйте и докажите для гиперболы утверждения, аналогичные утверждению из упражнения 1из темы эллипс.
Решение.
Другие рефераты на тему «Педагогика»:
- Философско-педагогические идеи представителей русского зарубежья
- Психолого-педагогические основы воспитательного характера
- Методические разработки внеклассных мероприятий в условиях компетентностного подхода в образовании
- Изучение влияния межпредметных связей на развитие письменной речи младшего школьника в процессе обучения русскому языку в 3 классе
- Методические особенности воспитания выносливости у детей 8–9 класса на уроках физической культуры
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
