Моделирование процессов статического конусообразования при разработке нефтяных, газовых и нефтегазовых залежей

Рис.2.7.Схема одновременного существования конусов газа и воды в условиях напорного притока к несовершенной скважине

Дифференцируя (2.20) по безразмерной ординате ξ=z/h и приравнивая полученное выражение нулю, находим ординату ξ* нейтральной линии тока. Вычисленные значения безразмерной ординаты нейтральной линии тока

ξ*=d/h

как функции параметров

α=a/h

и

β=b/h

приведены в табл.2.1 и представлены графиками на рис.2.8.

Таблица 2.1 Расчетные значения ординаты нейтральной линии тока ξ*

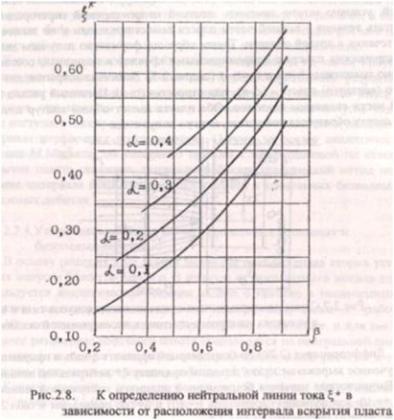
Отыскав таким образом ординату нейтральной линии тока 4*, по известным методикам можно рассчитать предельный безводный (для нижней части пласта) и предельный безгазовый (для верхней части пласта) дебеты, а затем предельную депрессию. Наименьший дебит из расчетных принимается как предельный безводный и безгазовый дебит скважины.

В соответствии с формулой (2.1) для удельного расхода

q0=Q/hft

по верхней и нижней частям пласта (см.рис.2.7) можно записать следующие соотношения [3,12,13]:

q01=εh1Δρ1

q02= (2.21)

где

Ђ1=;

Ђ2=;

h1=d;

h2=h-d

p01 = ;

p02 =;

ξ*=ε=

С учетом (2.22) формулы (2.21) принимают следующий вид:

q01=εhΔp1;

q02= ehΔp2. (2.23)

Безразмерные предельные дебеты q01(p1,Ђ1) и q02(p2,Ђ2) определяются по таблице (см.Прил. 1). Чтобы дебет был одновременно безводным и безгазовым, необходимо выбрать наименьший расход, т.е. принять q0=min {q01,q02}. Тогда предельный расход нефти через скважину будет

Q = q0(b-a) = q0(β-α)h . (2.24)

Очевидно, этот дебет в общем случае является предельным либо для конуса воды (и меньше предельного для конуса газа), либо для конуса газа (и меньше предельного для конуса воды).

Выражения в правых частях формул (2.23)

q1=q1(α,β,p0) =q( ). , (2.25)

q2=q2(α,β,p0)2 = ()2=q(, ()2 (2.26)

представляют собой соответственно безразмерные предельные безгазовые и безводные плотности расходов. С учетом (2.25) и (2.26) формулы (2.23) принимают вид

q01 = q1Δp1εh

q02 = q2Δp2εh . (2.27)

Для каждой пары значений а и В и соответствующих им значений ординат нейтральной линии тока (см.табл.2.1) по формулам (2.22) подсчитаны величины относительных вскрытий Ђ1,Ђ2 в зависимости от параметров а и В и значения параметров p01 и р02. Затем, с помощью таблицы (см.Прил.1) для предельных дебитов определялись q1(α,β,p0) и q2(α,β,p0), а затем по формулам (2.25), (2.26) рассчитывались плотности расходов q1 и q2. Результаты расчетов сведены в таблицу (Прил.З), которая охватывает все практически интересные значения параметров α, β, и р0[86]. В силу симметрии каждая строка таблицы дает одновременно значения безразмерных предельных плотностей расходов q1 и q2 для соответствующих значений α и β, т.е. qI,2(α,β)=q2,1(l-α,l-β). По данным таблицы нетрудно построить сетку кривых зависимостей q1,2=q1,2(p0) для фиксированных значений пары параметров а и В, т.е. для заданного интервала вскрытия (b-а), см.рис.2,7.

При конкретных расчетах предельных безводных и безгазовых дебитов поступают следующим образом. По известным параметрам а, 6 и р0 из таблицы или графиков находят плотности расходов qi и q2, затем по формулам (2.27) подсчитывают удельные расходы q01 и q02, из которых выбирают наименьшее значение q0=min{q01;q02}, и по формуле (2.24) подсчитывают искомый предельный дебит. Покажем применение метода на конкретных примерах.

 Скачать реферат