Растворение твердых веществ

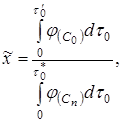(25)

где -время, необходимое для достижения в периодическом опыте.

В результате такой обработки экспериментальных данных получают зависимость доли нерастворившегося компонента eight=16 src="images/referats/13719/image008.png">от безразмерного времени

при постоянных концентрации активного реагента и температуре. Нетрудно убедиться в том, что, зависимость есть полный аналог кинетической функции . Аргументы х и отличаются друг от друга лишь постоянным множителем.

Действительно, из соотношени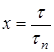й и 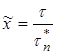следует, что

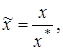(26)

где 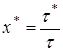- значение безразмерного времени х, отвечающее выбранной фиксированной величине . Соотношение (26) показывает, что зависимость сохраняет присущее кинетической функции свойство инвариантности относительно условий проведения процесса (поскольку величины х и не зависят от этих условий).

Переход от функции к кинетической функции эквивалентен простому изменению масштаба по оси абцисс. Это поясняется рисунком 2, где обе зависимости и - изображаються одной и той же кривой и различаются только масштабом по оси абцисс. В отличие от х, изменяющегося от 0 до 1, аргумент зависимости изменяется от 0 до некоторого значения .

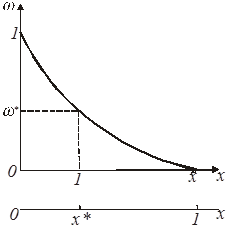
Рис.2. Зависимость доли нерастворившегося компонента от безразмерного времени .

На рис.2 безразмерное время пропорционально отношению , где - время, необходимое для достижения некоторого фиксированного значения .

Для получения кинетической функции достаточно разделить все значения на этот постоянный коэффициент . Предлагаемое видоизменение методики определения кинетической функции сводится к следующему:

1. Результаты каждого периодического опыта необходимо представить в виде зависимости доли нерастворившегося компонента и концентрации активного реагента от времени : и .

2. Выбирают некоторое фиксированное значение с таким расчетом, чтобы значению от 1 до соответствовали достаточно надежные участки всех экспериментальных кривых.

3. По уравнению (25) вычисляют значение , отвечающие ряду последовательных значений . Такие расчеты выполняют для каждого опыта.

4. Результаты расчетов используют для получения усредненной по всем опытам зависимости . Эту зависимость удобно нанести на график вместе с результатами обработки отдельных опытов и тем самым убедиться в инвариантности функции относительно технологических параметров процесса в исследованном диапазоне.

5. С помощью формулы:

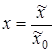(27)

необходимо перейти к обычной кинетической функции т.е. необходимо изменить масштаб по оси абцисс (рис.2).

Последний этап необходим для единообразия вычислительных процессов при переходе к их моделированию. Возможные значения безразмерного времени должны быть заключены в диапазон от 0 до 1. Поэтому использование кинетической функции , в которой аргумент нормирования в максимальной продолжительности процесса - времени полного растворения, предпочтительнее.

Заметим, что при растворении труднорастворимых веществ и выщелачивании чаще всего не достигают стопроцентного растворения или извлечения полезного компонента. В этом случае под временем полного растворения естественно понимать время достижения максимального возможного извлечения. Если обозначить максимально возможное извлечение через , то связь между долей нерастворившегося компонента и достигнутым извлечением опишется формулой:

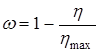(28)

Это значит, что при определении не следует принимать во внимание ту часть полезного компонента, которая не может быть переведена в раствор. Тогда изменению от 0 до (или х от 0 до 1) соответствует изменение от 1 до 0, что также благоприятствует единообразию вычислительного процесса.

 Скачать реферат