Элементы статистики, комбинаторики и теории вероятностей в основной школе

Для представления соотношения между частями некоторого единого целого, удобно пользоваться круговыми диаграммами. Для нашего примера она будет выглядеть следующим образом:

В 5 классе учащиеся должны уметь читать диаграммы. Для отработки таких умений нужно рассматривать задания следующего типа.

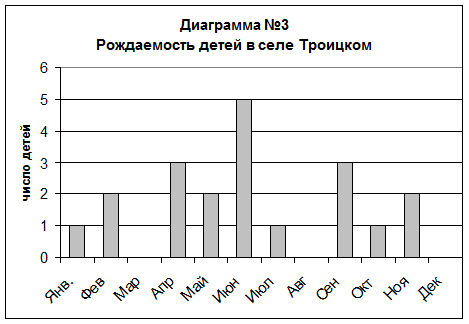
Используя диаграмму №3,

ответьте на вопросы:

1) в каком месяце в селе родилось больше всего детей?

2) В каком месяце родилось столько же детей, сколько в апреле?

3) В какие месяцы родилось по два ребенка?

4) Сколько детей родилось в марте?

5) Сколько детей родилось за первую половину года?

6) Сколько детей родилось за весь год?

§2. Методика реализации стохастической линии в 6 классе.

Основные задачи:

· Отработка умений и навыков в составлении и подсчете числа комбинаторных наборов.

· Показать учащимся как можно решать комбинаторные задачи с помощью рассуждений. Познакомить учащихся с правилом умножения при подсчете числа возможных вариантов, сформировать умения по его применению.

· Познакомить с правилом суммы

· Формирование умений строить дерево возможных вариантов.

· Формирование умений сравнения вероятностей разных событий (более вероятно, менее вероятно)

· Познакомить с понятиями статистической частоты и вероятности, с методом оценки вероятности через статистические испытания.

В 6 классе в теме комбинаторика продолжаем рассматривать комбинаторные задачи, на первый план выходят задачи по подсчету числа возможных вариантов.

Существует несколько подходов к преподаванию комбинаторики: теоретико-множественный, лексико-графический и теоретико-вероятностный. В школе преимущество отдается теоретико-множественному подходу, но будет полезным частично обратиться и к лексико-графическому подходу. При таком подходе все определения опираются на представление об алфавите, словах, длине слов и др.

Решая задачи, иногда очень удобно использовать кодирование, то есть обращение к лексико-графическому подходу.

Рассмотрим следующую задачу: несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг.

Мы можем записывать наше решение следующим образом : «1 вариант: первая полоса – красная, вторая – синяя, третья – белая.» и т.д. Но это очень долго и не удобно, записывая так, сложно сориентироваться все ли варианты мы записали, и не повторились ли мы где-нибудь. Поэтому очень удобно ввести кодирование, т.е. некоторое условное обозначение перебираемых в задаче объектов. В нашем случае мы заменим первой буквой каждый цвет полосы. Белый соответственно – «Б», красный – «К» и синий – «С».

Введя кодирование, запись решения задачи очень упрощается. Мы имеем множество из трех элементов {Б, К, С}. Нужно составить различные комбинации из трех элементов, при этом порядок элементов учитывается. Например, запись «БКС» будет обозначать, что первая полоса флага – белая, вторая – красная, третья – синяя. Подобные задачи мы уже решали методом непосредственного перебора и построением дерева возможных вариантов.

При встрече 8 приятелей обменялись рукопожатиями. Сколько всего было сделано рукопожатий?

Данную задачу можно решать методом непосредственного перебора, и уже в самом начале заметим, что довольно сложно перебирать все возможные варианты и не запутаться, не говоря уже о записи решения этой задачи. Но, введя определенные обозначения - кодирование, решение будет очень легко представить

Каждому приятелю даем номер от 1 до 8, а рукопожатия закодируем следующим образом: например число 24 означает что 2-ой приятель пожал руку 4-му. При чем число 35 и 53 означают одно и тоже рукопожатие, и брать будем меньшее из них. Коды рукопожатий мы можем оформить следующей таблицей:

12, 13, 14, 15, 16, 17, 18,

23, 24, 25, 26, 27, 28,

34, 35, 36, 37, 38,

45, 46, 47, 48,

56, 57, 58,

67, 68,

78.

Таким образом, у нас получилось 1+2+3+4+5+6+7=28 рукопожатий.

После того как учащиеся научились составлять всевозможные наборы, на первый план выдвигается задача подсчета числа возможных вариантов.

Группа туристов планирует осуществить поход по маршруту Антоново – Борисово – Власово – Грибово. Из Антоново в Борисово можно сплавиться по реке или дойти пешком. Из Борисово во Власово можно пройти пешком или доехать на велосипедах. Из Власово в Грибово можно доплыть по реке, доехать на велосипедах или пройти пешком. Сколько всего вариантов похода могут выбрать туристы? Сколько вариантов похода могут выбрать туристы при условии, что хотя бы на одном из участков маршрута они должны использовать велосипеды?

Построим для этой задачи дерево возможных вариантов:

Пусть у нас «П»-обозначает путь пешком

«Р» - сплавиться по реке

«В» - доехать на велосипедах.

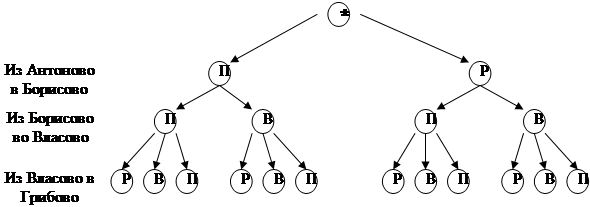
Ответ на второй вопрос также хорошо просматривается по дереву возможных вариантов.

Но эту задачу можно решить по-другому, с помощью рассуждений. Из Антоново в Борисово у нас 2 варианта каким образом продолжать путь, из Борисово во Власово тоже 2 варианта, т.е. на каждый вариант первого участка пути у нас есть по 2 варианта второго участка пути и того на данном этапе у нас будет 2*2=4 варианта выбора способа передвижения. На каждый из этих 4 вариантов существует по 3 варианта способа передвижения по третьему участку пути из Власово в Грибово, т.е. 4*3=12. Ответ в этой задаче мы получили умножением.

Такой способ подсчета называется правилом умножения, он возможен, если дерево возможных вариантов является «правильным»: из каждого узла выходит одно и тоже число веток.

От турбазы к горному озеру ведут 4 тропы. Сколькими способами туристы могут отправиться в поход к озеру, если они не хотят спускаться по той же тропе, по которой поднимались?

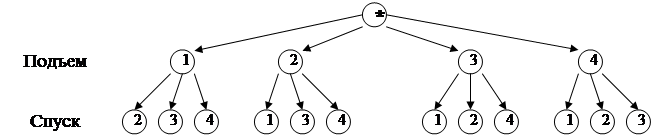Занумеруем тропы числами от 1 до 4 и построим дерево возможных вариантов:

Чтоб подняться у нас есть 4 тропы (4 варианта) и на каждый из них есть по 3 оставшихся тропы (3 варианта), чтоб спуститься, т.е. 4*3=12 маршрутов подхода к озеру. А теперь представим, что к озеру ведут не 4, а 10 троп. Сколько в этом случае существует маршрутов, если по-прежнему решено спускаться не по той тропе, по которой поднимались. Изобразить дерево возможных вариантов в такой ситуации очень сложно. Гораздо легче решить эту задачу с помощью рассуждений. Подняться к озеру можно по любой из 10 троп, а спускаться по любой из оставшихся 9 троп. Таким образом, всего получим 10*9=90 различных маршрутов похода.

Обе эти задачи мы решили, используя правило умножения, которое звучит следующим образом: пусть необходимо выполнить к независимых действий, если первое действие мы можем выполнить п1 способами, после чего второе действие можем выполнить п2 способами и т.д. до k-го действия, которое можно выполнить пk способами, тогда выполнить все k действия в указанном порядке можно п1∙ п2∙…∙ пk способами. Обратить внимание, что, применяя правило умножения, мы учитываем порядок действий. То есть правило умножения применяется для подсчета упорядоченных наборов.

 Скачать реферат