Деформация сдвига. Геометрические характеристики плоских сечений. Кручение стержней с круглым поперечным сечением

k ≥ (4F)/(πd2·τadm). (5)

При двухсрезном и многосрезном заклепочном соединении нужно вместо числа k в формулу (4) подставлять общее число срезов заклепок, расположенных по одну сторону стыка соединяемых листов.

Если на конструкцию действуют динамические, т.е. изменяющиеся с большой скоростью, например, ударные и вибрационные нагрузки, при расчете заклепочных соедине

ний на сдвиг необходимо учитывать неравномерность работы заклепок.

При соединении листов в конструкциях, представленных на рис. 5.14 не заклепками, а с помощью болтовых соединений, расчет болтов на сдвиг проводят аналогично приведенному расчету заклепок. Величины d и τadm будут соответственно обозначать диаметр болтов и допускаемое напряжение материала болтов на сдвиг (срез).

ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ

При рассмотрении деформации растяжения, сжатия, сдвига было установлено, что прочность и жесткость элементов конструкций зависит только от величины поперечного сечения и свойств материала элементов. При деформациях кручения и изгиба, при расчетах сжатых стержней на устойчивость, прочность и жесткость элементов конструкции зависят также и от формы их поперечного сечения. К числу геометрических характеристик сечения, учитывающих его размеры, форму и влияющих на прочность и жесткость конструкций, относятся статические моменты, моменты инерции и моменты сопротивления сечения.

Статические моменты сечения. Центр масс сечения

Статическим моментом сечения S относительно любой оси называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на их расстояние до этой оси. Так, статический момент сечения (рис. 3) относительно оси z:

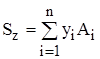, (6)

где Ai – площадь элементарной i– й площадки сечения, расположенной на расстоянии yi от оси z; n – число элементарных площадок сечения. При Ai → 0 (dA) и n → ∞

. (7)

Размерность статических моментов – длина в кубе. Статические моменты могут быть положительными, отрицательными и равными нулю.

Считая, что поверхностная плотность ρ* сечения постоянна, координаты центра масс сечения zc, yc можно выразить через статические моменты

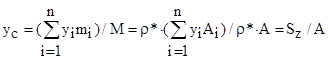, (8)

аналогично

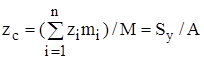, (9)

где mi – массы элементарных площадок сечения; М – масса сечения; А – площадь сечения; Sz и Sy – соответственно статические моменты сечения относительно координатных осей z и y.

Из выражений (8) и (9) видно, что при yc = 0; zc = 0, т.е. при прохождении координатных осей через центр масс С, статические моменты сечения относительно этих осей будут равны нулю, так как А ≠ 0. Такие координатные оси называют центральными. Это следствие можно выразить еще так: если статические моменты сечения относительно координатных осей равны нулю, т.е. Sz = 0, Sy = 0, то эти оси z, y проходят через центр масс сечения C.

Моменты инерции сечений

Полярным моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до данного полюса (точки). Из рис. 3

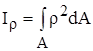, (10)

где ρ – расстояние от площадки dA до полюса (точки 0).

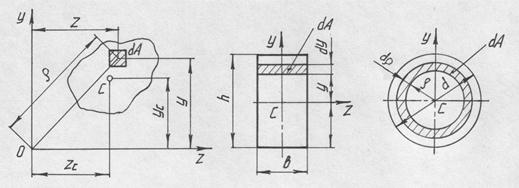
Рис. 3 и 4

Осевым моментом инерции сечения называется взятая по всей площади сечения сумма произведений площадей элементарных площадок на квадрат их расстояния до оси. Так, моменты инерции сечения относительно координатных осей z и y будут соответственно равны

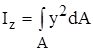, (11)

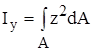. (12)

Так как ρ2 = z2 + y2, сравнив выражения (11), (12) и (13), получим

Iρ = Iz + Iy, (13)

т.е. сумма осевых моментов инерции сечения относительно двух взаимно перпендикулярных осей равна полярному моменту инерции этого сечения относительно точки пересечения рассматриваемых осей. Моменты инерции сечений – всегда положительные величины.

Моменты инерции прямоугольника, круга

Моменты инерции сечений вычисляются в следующей последовательности. Вначале находят момент инерции элементарной площадки dA относительно точки или оси. Считая, что число таких площадок стремится к бесконечности, далее вычисляют сумму моментов инерции площадок по всему сечению. Чаще всего детали типа стержней имеют форму поперечного сечения в виде круга или прямоугольника.

Вычислим момент инерции прямоугольника (рис. 4, а) с основанием b и высотой h относительно оси z, проходящей через центр масс параллельно основанию. За элементарную площадку dA примем площадь бесконечно тонкого слоя dA = bdy. Тогда

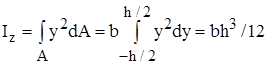. (15)

Аналогично получим

Iy = hb3/12. (16)

Рассмотрим круг (рис. 5.16, б). Сначала определим полярный момент инерции круга относительно геометрического центра С: .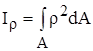

За элементарную площадку dA примем площадь бесконечно тонкого кольца толщиной dρ: dA = 2πρdρ. Тогда

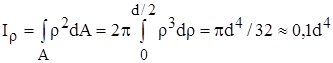. (17)

Найдем моменты инерции круга относительно координатных осей y, z, проходящих через центр масс С. Так как оси являются диаметром круга, то Iy = Iz. Поэтому выражение (5.38) можно представить как Iρ =2 Iy = 2 Iz, откуда

Iy = Iz = Iρ/2 ≈ 0,05 d4. (18)

Для кольца моменты инерции равны разности моментов инерции внешнего и внутреннего кругов с диаметрами соответственно d и d1.

Тогда

Iρ ≈ 0,1 (d4 – d14), (19)

Iy ≈ Iz ≈ 0,05 (d4 – d14). (20)

КРУЧЕНИЕ СТЕРЖНЕЙ С КРУГЛЫМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ

Понятие о крутящем моменте

Деформация кручения происходит при действии на стержень внешних пар сил, плоскости действия которых перпендикулярны оси стержня. При этом в поперечных сечениях стержня возникает только одна составляющая внутренних сил – крутящий момент Т. С явлением кручения встречаются при расчете валов, винтовых пружин и других элементов конструкций.

Если прямые незакрепленные стержни, подвергающиеся деформации кручения, равномерно вращаются или находятся в покое, алгебраическая сумма всех внешних скручивающих (вращающих) моментов Те равна нулю.

 Скачать реферат