Разработка лекционной демонстрации "Изучение механизма формирования ударной волны" для курса "Молекулярная физика"

Из уравнения (2.4) получим

(2.13)

Исключая из первых двух уравнений (2.4)-(2.5) сначала одну, а потом другую скорость, найдем

(2.14)

(2.15)

Если ударная волна создается в покоящемс

я газе движением поршня,

для скорости движения сжатого газа относительно невозмущенного, равной скорости «поршня», получим формулу

(2.16)

Отметим полезную формулу для разности кинетических энергий газа по обе стороны разрыва в системе координат, в которой разрыв покоится:

(2.17)

Подставляя выражения для квадратов скоростей (2.14), (2.15) в уравнение энергии (2.4), получим соотношение, связывающее давления с удельными объемами по обе стороны разрыва:

(2.18)

Заменяя удельные внутренние энергии на удельные энтальпии по формуле , перепишем эту формулу в другом виде:

(2.19)

По аналогии с соотношением, связывающим начальные и конечные давления и объемы при адиабатическом сжатии вещества, выражения (2.18) или (2.19) носят название ударной адиабаты или адиабаты Гюгонио.

Ударная адиабата представляется функцией

(2.20)

которая в ряде конкретных случаев, когда термодинамические связи выражаются простыми формулами, может быть найдена в явной форме.

Ударная адиабата имеет существенное отличие от обычной адиабаты (адиабаты Пуассона в идеальном газе с постоянной теплоемкостью). В то время как последняя представляет собой однопараметрическое семейство кривых p = P(V,S), где параметром служит только значение энтропии S, адиабата Гюгонио зависит от двух параметров: давления и объема в начальном состоянии ро, Vo. Чтобы исчерпать все кривые р = Р(V,S), достаточно пройти одномерный ряд значений энтропии S. Чтобы исчерпать все кривые , надо построить «бесконечность в квадрате» кривых, отвечающих всем возможным р0 и V0.

Ударные волны в идеальном газе с постоянной теплоемкостью

Особенно простой вид приобретают формулы для ударной волны в случае идеального газа с постоянной теплоемкостью. На этом примере удобно выяснить все основные закономерности изменения величин в ударной волне. Подставим в уравнения ударной адиабаты (2.18) или (2.19) соотношения

(2.21)

Это дает возможность найти в явном виде уравнение ударной адиабаты:

(2.22)

Для отношения объемов получим формулу:

(2.23)

Отношение температур равно

(2.24)

С помощью (2.23) скорости по формулам (2.14) и (2.15) можно представить через давления и начальный объем:

(2.25)

(2.26)

Выясним на примере идеального газа с постоянной теплоемкостью некоторые закономерности для ударных волн. Ударная адиабата представляет собой кривую на плоскости р, V, которая проходит через точку начального состояния р0, V0.

Эта кривая изображена на рис. 2.3. В принципе формулу (2.22) можно распространить и на давления, меньшие начального Эта часть кривой соответствует физически неосуществимым состояниям. Поэтому она проведена на рис. 2.3 пунктиром.

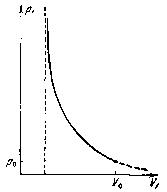
Рисунок 2.3 — Ударная адиабата

Из формулы (2.23) видно, что в случае ударной волны очень высокой амплитуды, когда давление за фронтом гораздо больше начального, плотность газа при возрастании амплитуды увеличивается не беспредельно, а стремится к определенному значению. Это предельное сжатие в ударной волне зависит только от показателя адиабаты и равно

(2.27)

Для одноатомного газа с предельное сжатие равно 4. Для двухатомного газа в предположении, что колебания не возбуждены, y = 7/5, и предельное сжатие равно 6; если считать, что колебания возбуждены, и сжатие равно 8. В действительности, при высоких давлениях и температурах теплоемкость и показатель адиабаты в газах уже не являются постоянными, так как в газе происходят диссоциация молекул и ионизация атомов. Сжатие газа в ударной волне при данном большом отношении давлений тем сильнее, чем выше теплоемкость и меньше показатель адиабаты.

Поскольку при больших давлениях р1 плотность возрастает очень медленно с ростом давления, температура сжатого газа растет пропорционально давлению (см. формулу (2.24) при ). В пределе сильной волны, когда

(2.28)

Скорости в пределе при растут пропорционально корню из давления. Как видно из формул (2.18) и (2.19), при

(2.29)

Очень важные следствия можно получить, сопоставляя скорости газа по обе стороны разрыва с соответствующими скоростями звука. В идеальном газе с постоянной теплоемкостью

. (2.30)

Составим отношения скоростей газа относительно разрыва к скоростям звука:

, (2.31)

, (2.32)

В предельном случае ударной волны малой амплитуды, когда давления по обе стороны разрыва близки друг к другу, , , согласно формуле (2.23), также мало и сжатие газа: ; близки друг к другу и скорости звука . Из формул (2.31) и (2.32) видно, что в этом случае . Но u0 есть скорость распространения разрыва по невозмущенному газу. Таким образом, слабая ударная волна бежит по газу со скоростью, очень близкой к скорости звука, т.е. практически не отличается от акустической волны сжатия. Это не удивительно, ибо при малом отличии p1 от р0 мы имеем дело с малым возмущением.